Abstract
In this paper we present a statistical method for inferring historical social
networks from biographical documents as well as the scholarly aims for doing so.
Existing scholarship on historical social networks is scattered across an
unmanageable number of disparate books and articles. A researcher interested in
how persons were connected to one another in our field of study, early modern
Britain (c. 1500-1700), has no global, unified resource to which to turn.
Manually building such a network is infeasible, since it would need to represent
thousands of nodes and tens of millions of potential edges just to include the
relations among the most prominent persons of the period. Our Six Degrees of Francis Bacon project takes up recent
statistical techniques and digital tools to reconstruct and visualize the early
modern social network.
We describe in this paper the natural language processing tools and statistical
graph learning techniques that we used to extract names and infer relations from
the Oxford Dictionary of National Biography. We
then explain the steps taken to test inferred relations against the knowledge of
experts in order to improve the accuracy of the learning techniques. Our
argument here is twofold: first, that the results of this process, a global
visualization of Britain’s early modern social network, will be useful to
scholars and students of the period; second, that the pipeline we have developed
can, with local modifications, be reused by other scholars to generate networks
for other historical or contemporary societies from biographical documents.
Introduction
Historians and critics have long studied the ways that early modern writers and
thinkers associated with each other and participated in various kinds of formal
and informal groups. Although their findings have been published in countless
books and articles, there is currently no way to obtain a unified view of the
early modern social network. A scholar must start largely from scratch if she
seeks to understand complex relations between multiple people, identify
potentially important relationships that have yet to be explored, understand the
extent of communities of interaction, or visualize the scholarly consensus
regarding networks, whether small or large. The creation of a large scale early
modern social network gives scholars a visual way to explore scholarly knowledge
of relationships and to see what has – or hasn’t – been studied in the extant
historiography.
The most desirable outcome of our work would of course be a comprehensive map of
the way early modern persons were related. Yet practical challenges abound. The
population of Britain rose to over 5.5 million people by the end of the
seventeenth century, and little documentary evidence survives on much of that
population. Attempting to reconstruct the full network would be unrealistic.
Even if we limited ourselves to people alive in 1700 and successfully gathered
5.5 million names, the number of potential relationships in that set exceeds 15
billion. Social relations are exceedingly complex, even in societies
considerably smaller than our own. There are thus excellent reasons to proceed
more conservatively–focusing only on small, well-documented subsets of the
population. Some of the best known digital networks projects, such as Stanford
University’s
Mapping the Republic of Letters and
Oxford University's
Cultures of Knowledge, do just
that. Adhering to historians’ venerable practice, they proceed incrementally and
only include relationships directly attested by documents such as letters. This
approach produces relatively small, highly substantiated networks – on the order
of, say, 500 nodes [
Ahnert and Ahnert 2014]
[
Basu et al. 2015] – but it also limits these networks to representing an
infinitesimal sliver of the rich and varied kinds of relationships between
people.
Taking a different approach, we identified biographical data as the most
productive starting point for our network reconstruction, which we have named
Six Degrees of Francis Bacon (SDFB), after the
early modern figure whose life spanned the sixteenth and seventeenth centuries
and whose career spanned the domains of politics, science, and letters. We chose
biographies because they are a well-established and highly standardized product
of modern historical scholarship. Moreover, a central collection of such data
was already available to us digitally through the
Oxford
Dictionary of National Biography (ODNB), which comprises the
biographies of people deemed by its editors as significant to British history.
Jerome McGann has argued that “the whole of our cultural
inheritance has to be recurated and reedited in digital forms and
institutional structures”
[
McGann 2014, 1]. Most often, in his account, this involves
transference of
text “from bibliographical to digital
machines.” SDFB tackles a related but more difficult problem: the
transformation of biographical text, which focuses on a single
person but contains rich information about social relations, into a global
(non-egocentric) network graph, which requires extracting information about
nodes (persons) and edges (relations) while ignoring or discarding other kinds
of biographical information.
From the ODNB biographies of persons who lived between 1500-1700 we created an
initial dataset of 13,309 actor nodes. Each actor node could potentially be
connected to any of the other nodes, leading to over 88 million potential edges
to explore. Even within this initial dataset, already limited for manageability,
it was not feasible to verify each potential edge. One approach might have been
to curate these relationships in an ad-hoc order, as a scholar became interested
in a particular relationship or as relationships were explicitly documented in a
scholarly source. We would then have collected as many relationships as the time
and labor of scholars allowed, but we would have had little to say about the
relative importance of collected relationships and nothing at all to say about
those relationships yet to be curated. For instance, would the absence of an
edge mean that the two nodes shared no association or that the association has
yet to be explored in our network? Rather than rebuilding the network by hand,
we chose to employ a computational and statistical approach, unifying the
dispersed knowledge already extant in the literature into an inferred graph of
the network that can then be made available to scholars for correction and
curation.
In the following sections, we lay out our statistical method for reconstructing
the early modern social network in four broad steps, then examine the
significance and limitations of our results from the perspective of humanist
scholarship. In section one, we discuss the process of identifying a collection
of textual documents to use as input, considering both direct and indirect
evidence of historical relationships. In section two, we explain how we used
Named-Entity Recognition (NER) to process the unstructured text into structured
data – specifically a matrix of documents and named entities – that was amenable
to statistical analysis. In section three, we give an overview of how we applied
statistical graph-learning methods to our structured data, with more detailed
technical information included an appendix. In section four, we discuss methods
of validating a sample of proposed relationships using the local expertise of
humanist scholars. In section five, we step back to examine the broader
significance of this process from the perspective of twenty-first-century
researchers in the humanities. We also examine the assumptions underlying our
statistical methods and potential areas of modification necessary before
redeploying these methods with other historical corpora.
In developing this method, we have demonstrated the feasibility of applying graph
learning methods to any large collection of biographical text – early modern or
otherwise. This is neither a completely automated process nor a perfect one, but
we have also developed a practical mechanism by which expert feedback can
improve the network as well as the statistical procedures used to infer it. We
have thus created a viable and transferrable approach to inferring large-scale
historical social networks, which should be of particular interest to digital
humanists, scholars of networks and prosopography, as well as scholars
interested in the history of scholarship itself.
1. Source Material
The first step of our process was identifying the extent of available texts and
determining which texts were potentially the most useful for network inference.
Numerous types of primary and secondary sources can provide evidence of
historical relationships. Some of these sources provide direct evidence of a
link between two actors – for example, society membership rolls, marriage
certificates, or archival letters. Other sources may collectively provide
indirect evidence: the same two people mentioned together in numerous accounts
or biographies is highly suggestive of the possibility that those two people may
have come into contact with one another.
In an ideal world we would have made use of all the relevant historical sources
and scholarship. In this one, we needed to begin with a collection of texts that
was well-defined, accessible, machine readable, and relatively uniform. We also
wanted to begin with a collection that included a broad range of potentially
relevant figures, according to social, geographic, and temporal standards. We
therefore decided to focus on the 58,625 biographical entries that make up the
ODNB. Running to sixty volumes in its print format, the ODNB is the labor of
10,000 scholars who have collectively contributed its 62 million words.
On a technical level, the ODNB was praised upon its 2004 release for being “the first to exploit the
potential of electronic publication on so vast and imaginative a
scale”
[
Collini 2005]. We considered the ODNB an appropriate choice for several other reasons
as well. Several of the collaborators on this project share a primary interest
in the early modern era (c. 1500-1700) in Britain, a period well covered by the
ODNB. Both Carnegie Mellon University and Georgetown University have
subscriptions to the ODNB, providing us with legal access to the “many possibilities opened up by
the online version for accessing and organising the hoard of
information”
[
Collini 2005]. The ODNB’s dense-in-data documents fit the criteria of machine
readability and relative uniformity. Although the biographies vary in length,
all have a similar format and the raw text can be extracted in the same manner.
Lastly, as biographies, they contain both explicit mentions of relationships –
such as “Bacon’s life and career
during the 1590s was dominated by his close relationship with Robert
Devereux” – as well as numerous implicit indicators of potential
relationships. Robert Cecil, for example, is mentioned five times in one section
of Bacon’s biography [
Peltonen 2004]. The ODNB thus offered
opportunities to analyze both direct and indirect relationship data from a
single collection.
As we worked with the ODNB data, a further advantage of this particular
collection emerged: its ability to shed light on the current state and history
of scholarship. Individually, each document in the ODNB is a roughly
chronological account of one person’s life, specifically an individual deemed by
nineteenth-, twentieth-, or twenty-first-century editors to have “in some way influenced [British]
national life”
[
Collini 2005]. As a collection, therefore, the ODNB holds significant information about
what has and has not risen to the level of scholarly notice since the late
Victorian creation of the Dictionary of National Biography, the ODNB’s
precursor, in the 1880s. The original DNB primarily emphasized the political,
literary, and scientific accomplishments of famous men, dedicating only 5% of
its overall entries to women, and only 2% of the entries in the target date
range 1500-1700. In the ODNB’s current version, the percentage of women has only
increased to 11% overall and 6% in our target date range [
Matthew and Harrison 2004].
In our era of text mining and network visualizations, such biases have continued
effects. A bias towards men is a known issue in existing historiography; this
bias is neither confined to the ODNB nor particularly surprising. However,
transforming textual secondary sources into visual representations allows for
more purposeful “critical scrutiny of what is
known, how, and by whom” – the branch of knowledge increasingly
referred to as “metaknowledge”
[
Evans 2011]. Our visualizations of the early modern social network demonstrate the
need both for more scholarship on women and other marginalized groups and for
the integration of this scholarship into broader discussions of earlier modern
society and culture; more importantly, it identifies the local areas of the
network where the need for such scholarship is most pressing.
2. Pre-Processing Source Material
After having identified our collection of source materials, we then had to
process the unstructured text – specifically a collection of HTML-formatted
documents acquired through the ODNB website – into a format more amenable for
analysis. This was done by extracting only the biographical portions of the text
from the initial HTML documents – stripping the HTML formatting, bibliographies,
and other extraneous text from the documents.
[1]
We then ran the plaintext documents through two NER tools: one from Stanford’s
Natural Language Processing Group, denoted Stanford [
Finkel et al. 2005],
and another from the LingPipe collection of tools [
Alias-i 2008].
These NER tools use probabilistic methods to identify names and to classify
those names according to types such as person, location, or organization. For
example, the following sentence – “The occasion
of ‘Lycidas’ was the death of Edward King, a fellow of Christ's College who
had drowned off the coast of Anglesey on 10 August 1637” – might be
processed as “The occasion of
‘[PERSON]Lycidas[/PERSON]’ was the death of [PERSON]Edward
King[/PERSON], a fellow of [ORGANIZATION]Christ's College[/ORGANIZATION]
who had drowned off the coast of [PLACE]Anglesey[/PLACE] on [DATE]10
August 1637[/DATE]”
[
Campbell 2004]. This example shows that no classifier is perfect – “Lycidas” in fact is the title of Milton’s great elegy rather than an
historical person – and classifiers face particular challenges with
multiple-word entities such as “Christ’s College” where the the first word
separated from its follower could mistakenly if understandably be classed as a
person.
For both Stanford and Lingpipe, we began with the default models trained on news
article corpora and ran the tools on ten randomly chosen documents from the
ODNB. These documents were then manually tagged to determine the accuracy of the
tools’ performance on our target dataset. Two measures of accuracy were used:
recall, the fraction of desired results obtained, and precision, or the fraction
of obtained results that are correct. For our purposes, high recall was
considered necessary, while high precision was desirable but less important.
Stanford achieved better recall than LingPipe, at 70.7% and 67.8% respectively,
but combining their results led to recall rates of 85.7%. The two tools were
combined by taking all of Stanford’s smatches, and then adding in LingPipe’s
matches if Stanford did not tag those specific words. In case of overlapping or
contradictory tags, we used Stanford’s matches.
| Subset |
Recall |
Precision |
Stanford (ST), Person Tags Only
LingPipe (LP), Person Tags
Only |
63.51%
52.44% |
91.75%
72.11% |
ST, Person and Organization Tags
LP, Person and Organization
Tags |
70.74%
67.83% |
74.02%
46.19% |
ST + LP, Person Tags Only
ST + LP, Person and Organization
Tags |
79.37%
85.66% |
77.91%
51.61% |
Table 1.
Recall and Precision for Various Subsets of NER Results
We then implemented two additional procedures to improve recall and precision.
First, to improve recall, we ran the documents through NER twice: once to create
the initial tags and a second time using the initial tags as a dictionary, which
enabled us to search for missed instances of phrases that were tagged during the
first pass through the documents. This latter search was particularly successful
at capturing partial name co-references, which occur within documents when
historical figures are referred to only by their first or last name. With few
exceptions, partial names that are part of a longer name found in that document
are not actually different people. “Bacon” in a document containing
“Francis Bacon” will refer, except in rare cases, to Francis Bacon. If
a partial name matched the subject of a biography, it was considered a mention
of that subject. Otherwise, partial names were considered mentions of the
matching most recent full-name mention.
Second, to improve precision, we implemented manual rules to reduce the number of
non-human names detected. This included removing all phrases that contained
words beginning with lower-case letters; exceptions were made for the words
“of” and “de” which often form part of names during this period,
i.e. “Katherine of Aragon.” We also eliminated phrases with non-alphabetic
characters – such as $, *, and numbers – and common non-human proper names
supplied by our subject matter experts – such as “Commonwealth,”
“Catholic,”
“Greek,” and “Roman.”
This resulted in final recall rates of 96.7% and precision rates of 65.5% on the
initial test set. Testing on six new randomly-chosen documents led to a similar
95.3% recall rate but a slightly lower 54.0% precision rate. As our priority was
a high recall rate, this was deemed acceptable. A later examination of a random
200-entity sample indicated the overall dataset’s precision rates were
approximately 59% with +/- 7% margin of error.
From these results, we created a large table of documents and named entities.
For each document, we tabulated the named entities and their number of mentions,
which led to 494,536 different named entities occurring throughout the
collection of 58,625 documents. We then reduced the number of named entities in
two ways. First, we ignored named entities that did not occur in an ODNB
biography within the period of interest (1500-1700). This made network inference
less costly computationally. So too with our second step, in which we omitted
names that occurred in fewer than five documents. Since correlations are very
difficult to determine with sparse data, inferring relations among low count
documents would have increased the number of false positives. While the five
mention threshold did unfortunately mean that we had to eliminate many less
prominent individuals, or those referred to by different names across the ODNB,
the tradeoff was that it helped us achieve better precision at less
computational cost. A final stage required further human curation –
specifically, searching for names in the ODNB – to disambiguate people who
shared the same name and de-duplicate people referenced under multiple names,
particularly for names obtained through the NER tools. While recent research in
the NLP community has focused on finding a way to automate this final stage,
such as the Berkeley Entity Resolution System, we preferred the accuracy of
manual curation [
Durrett and Klein 2014].
The resulting table of 58,625 rows and 13,309 columns is known mathematically as
a matrix. This n×p matrix, Y, has n rows
representing documents and p columns representing people, or
actors, in the network. The number of times person j is mentioned
by name in document i gives us Yij, a
non-negative integer for each document/person pair. We used this document-count
matrix to infer the social network.
3. Statistical Inference
We motivated our statistical model for the previously described document-count
matrix by assuming that direct connections between historical figures would be
reflected by their being mentioned together in documents. Indeed, prior work has
shown it possible to infer a rough graph based on co-mentions alone [
Bosch and Camp 2011]
[
Bosch and Camp 2012]. However, our model requires more than a simple count
of co-mentions because co-mentions sometimes result from confounding factors
such as mutual acquaintances.
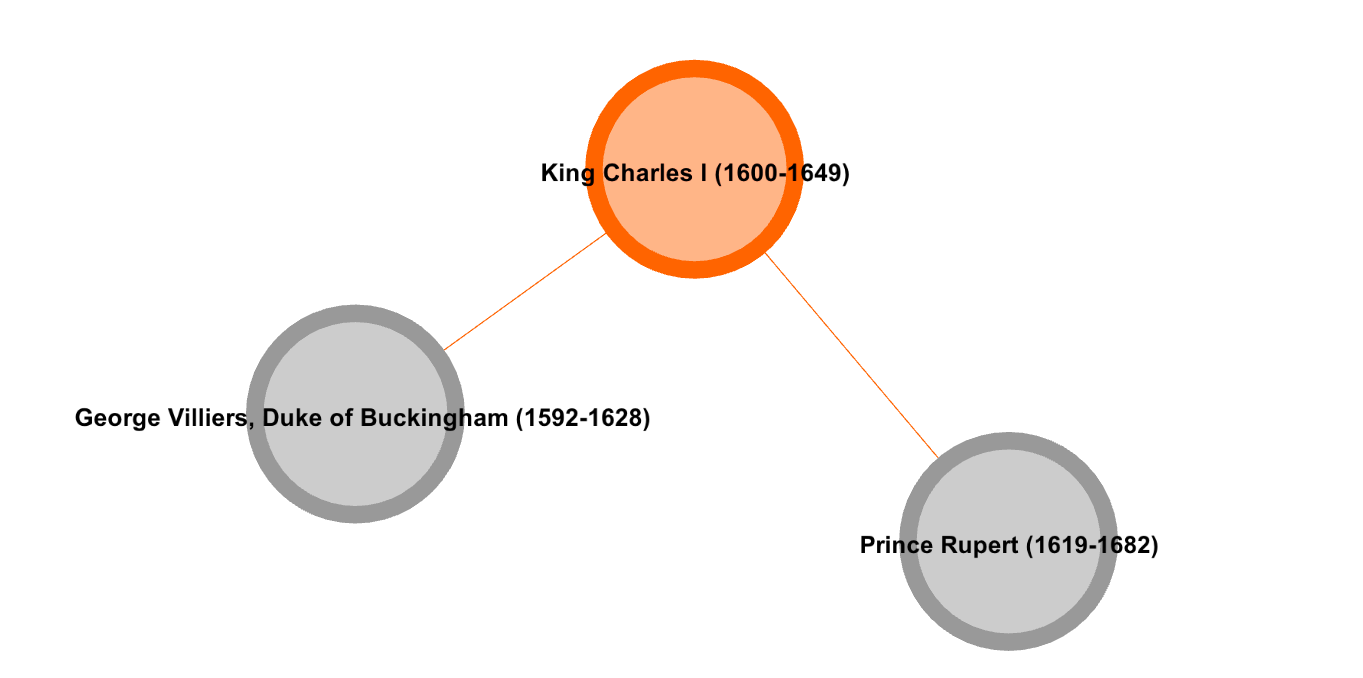
Consider an example such as the one displayed in Figure 2. George Villiers, Duke
of Buckingham (1592-1628), knew King Charles I (1600-1649), and Charles I knew
Prince Rupert of the Rhine (1619-1682), but Buckingham and Prince Rupert – whose
lives only barely overlapped – never met. Because Prince Rupert and Charles I
are connected, they will tend to be mentioned together in source documents. How
often Prince Rupert is mentioned can therefore be predicted in part from how
often Charles I is mentioned. Likewise if Charles I and Buckingham are
connected, mentions of Buckingham predict mentions of Charles I. But in the case
of no direct tie between Prince Rupert and Buckingham, as here, their names may
still correlate due to mentions of Charles I. Despite such correlation, mentions
of Buckingham convey no information about mentions of Prince Rupert not already
accounted for by mentions of Charles I. We thus reasoned that co-mentions found
in our document-count matrix – and correlations between any two given nodes
derived from the matrix – might be the result of one or more confounding
factors.
Under these assumptions, inferring the existence of network connections is the
same problem as inferring the conditional independence structure in a particular
statistical model – in this case, our document-count matrix [
Glymour et al. 2001]. The method we used to infer the conditional
independence structure of the document-count matrix is the Poisson Graphical
Lasso, a penalized regression method proposed by Allen and Liu. This method is a
generalization of Meinshausen and Bühlmann’s computationally faster
approximation to the graphical lasso [
Friedman et al. 2008]; it defines
the relationships between nodes by a conditional Poisson distribution, instead
of a multivariate normal distribution, which allows the penalized regression to
be modified by an individual node’s count data [
Allen and Liu 2012]. This
method allowed us to create a symmetric
p×
p correlation matrix
θ̂, where two
nodes
j and
k are conditionally
independent if and only if the coefficient
θ̂jk =
θ̂kj is zero.
In some applications of graphical models to infer network structure, all non-zero
coefficients are of interest. For example, in gene networks, the expression
levels of two connected genes may be negatively (conditionally) correlated. In
our social network, however, we are primarily concerned with positive
coefficients, as a relationship between two people should lead to a positive
conditional correlation of their mentions in a document. A small or zero
correlation suggests a lack of relationship between two people, while negative
correlations might occur for a variety of reasons, including non-overlapping
lifespans or two-degree – i.e., friend-of-a-friend – relationships without
so-called triadic closure [
Simmel 1950].
We therefore used our initial correlation matrix to create an adjacency matrix Y
– a symmetric p×p matrix where
Yij=Yji=1 when there is
a positive correlation and assumed relationship between person i and person j, and 0 otherwise. Because our
data and methods provide more information about some edges than others, however,
we wanted to be able to attach a confidence estimate to potential edges instead
of simply obtaining a yes or no estimate.
Confidence estimates were also better suited to the grey areas of humanistic
research often requiring interpretation and even guesswork. In order to create
this confidence estimate, we fit the Poisson Graphical Lasso on random subsets
of our data 100 times and added the resulting adjacency matrices into a final
matrix that we called our confidence matrix, C. This calculation gave us a
“confidence level” for the likelihood of a relationship’s existence
that ranged between 0 – never inferred – and 100 – always inferred.
Throughout this process, we experimented with tuning parameters and found that
our final estimates did not vary significantly for all reasonable tuning
parameters, where reasonable is defined as a low enough penalty such that edges
are actually added, but high enough penalty that the algorithm converges
rapidly. We also conducted penalty parameter training – using expert knowledge
to manually confirm the existence of some relationships – but found this
produced only very localized changes and had little impact on the overall
network structure. The only significant manual intervention in this basic method
thus came from our name disambiguation procedures, as we had nearly one thousand
non-unique names in our node set. To deal with the the challenge of multiple
individuals sharing the same name, we first disallowed positive adjacency
estimates between two people with non-overlapping lifespans (with a one-year
margin of error for posthumous children). Second, we used probabilities based on
biography length to distribute adjacency estimates among people with overlapping
lifespans.
A fuller explanation of our application of the Poisson Graphical Lasso can be
found in our
Appendix, along with a link to our code.
4. Expert Validation
Having constructed our confidence matrix of estimated relationships, we then
conducted three different types of validation checks: one to ensure that our
results showed the homophily that network studies have taught us to expect when
semantic context is taken into account; one to confirm that our results were
consistent with statistical theory; and one to evaluate the accuracy of our
results in comparison with an expert human reading of the ODNB biographies. We
first used topic modeling on approximately 90% of our dataset – excluding people
with duplicate names whose relationships had to be disambiguated – to evaluate
different kinds of actor connectivity in a semantic context. Then, on smaller
subsets of our data, we compared our results with alternative statistical
methods, and calculated precision and recall rates.
Our first validation step was motivated by the fact that the Poisson Graphical
Lasso counts names but ignores semantic context. As a way to test the validity
of this approach, we wanted to compare the connectivity of actors who are
mentioned in similar contexts to the connectivity of those mentioned in
different contexts, since actors who share contexts are more likely to know one
another than those who do not [
McPherson, Smith-Love and Cook 2001]. Thus for our first
validation step, we decided to create and analyze a latent dirichlet allocation
(LDA) topic model – an algorithm for extracting semantic clusters from a set of
text [
Blei et al. 2003]
[
Weingart 2012]. We hoped to find our network data showed greater
connectivity between actors who share a context than between actors in different
contexts, as generated through the topic model. If so, we could conclude that
our approach produces results compatible with accepted, semantically-sensitive
approaches.
To generate our topic model, we created a ‘bag of words’ for each person in our
dataset, comprised of all words that appear before and after the person’s name
in the ODNB. Specifically, for each person in the network, we located all
mentions in the ODNB, and used the previous fifteen words and next twenty-five
words – excluding named entities – as their “bag of words”. The choice of
these two numbers was motivated by attempting to capture the current sentence
and the previous and next sentences. We then removed all named-entity mentions
in these biographies and converted the remaining words into lower case. Next we
applied the Porter stemmer [
Porter 1980], an algorithm that strips
away standard English suffixes in a specific order. For example, the Porter
stemmer turns the word ‘publisher’ into ‘publish’, and does same to the word
‘published’. We then dropped words that are in a standard stoplist – which
includes words like ‘and’, ‘the’, etc. – provided in the text-mining R package
tm [
Feinerer et al. 2008]. In addition, we dropped all month words, some
numbers, and select relationship terms – a complete list can be seen in our
topic modeling R code.
[2]
The remaining words in the ‘bag of words’ for each person thus approximately
reflected their profession, accomplishments, or “historical significance”
as given by the ODNB.
Using each of these “bags of words” as an individual text, we fit three
topic models to our collection of texts.
[3] The three topic models were generated with
five, ten, and twenty topics, respectively, to ensure the number of topics did
not significantly alter our results. The topics were generated automatically and
each text – and the person it represents – was assigned to the topic with the
highest probability match. The top representative terms in our ten-topic model
can be seen in Figure 3. The clustering of historical subjects and people in our
topics is encouraging, as many of the topics clearly represent different kinds
of historical activities. For example, Topic 3 in our ten-topic model contains
the words “bishop,”
“church,”
“minist” and “preach”, as well as a large number of churchmen such as
Richard Bancroft and John Whitgift (see Figure 3). Topic 8 includes the words
“publish”, “poem”, and “play,” along with poets like Robert
Herrick, John Donne, and John Dryden.
| Topic 1 |
Topic 2 |
Topic 3 |
Topic 4 |
Topic 5 |
london
famili
merchant
coloni
trade
work |
earl
lord
parliament
second
king
london |
bishop
colleg
church
minist
preach
london |
armi
command
return
forc
captain
ship |
work
publish
letter
write
public
book |
| Topic 6 |
Topic 7 |
Topic 8 |
Topic 9 |
Topic 10 |
king
polit
parliament
appoint
duke
lord
|
work
london
publish
book
print
physician
|
work
publish
poem
play
translat
edit
|
earl
london
famili
marriag
second
will
|
king
queen
english
england
court
royal
|
Table 2.
A table of the top representative terms in the ten-topic model
We then analyzed the frequency of our estimated relationships between people who
do and do not share topics. For all three topic models, estimated relationships
between people who shared a topic are more frequent than between-topic estimated
relationships; the specific results for the ten-topic model can be seen in
Figure 4. This coincides with the expectation for homophily (also known as
assortativity) and a qualitative, semantics-based reading of the same data: book
authors are more likely to be linked to other notable authors as opposed to
notable military personnel. While running a topic model with different
parameters (i.e. number of topics) changes the specific results, within-topic
relationships remain more frequent than between-topic relationships. We
therefore concluded that the Poisson Graphical Lasso produces results compatible
with other, semantically-sensitive methods.
| Measure |
Within-Topic |
Between-Topic |
| Fraction of Edges with Confidence ≥ 90% |
0.0001444 |
0.0000117 |
| Fraction of Edges with Confidence ≥ 75% |
0.0004523 |
0.0000527 |
| Fraction of Edges with Confidence ≥ 50% |
0.0016402 |
0.0003082 |
| Fraction of Edges with Confidence ≥ 30% |
0.0033207 |
0.0007585 |
Table 3.
A table of relationship confidence estimates in the ten-topic model
Our second validation step was to compare our results with alternative methods of
constructing a confidence matrix. Using Spearman correlations, which measure how
well the ordering of two ranked lists align, we evaluated how each method
performed against expert-generated ranked relationship lists. We had earlier
considered using three possible methods for inferring a correlation matrix from
the document-count matrix: 1) ranking by simple correlation (high positive
correlations are higher ranked relationships); 2) running the Poisson Graphical
Lasso and ranking edges by the value of ϱ in which the edge was added to the
model (edges added with more penalization are higher ranked relationships); and
3) running the Poisson Graphical Lasso and ranking edges by the value of the
regression coefficient (higher positive coefficients are higher ranked
relationships). According to statistical theory, both versions of the Poisson
Graphical Lasso should perform as well as, if not better than, simple
correlation because of their ability to screen off friend-of-a-friend
connections, as described in section three above. We hoped to find this
reflected in our Spearman correlations, in order to conclude that our approach
produces results compatible with statistical theory.
We chose to test this on James Harrington and John Milton by taking the top
thirty relationships according to each of these three methods and combining them
to create a master list of thirty and eighty relationships, respectively.
Faculty and PhD students with backgrounds in the early modern period were given
the combined names in random order and asked, first, to rank the relationships
according to a question we used to approximate relationship importance,
specifically “how unhappy would experts be if this relationship were not
included among the main actor’s top relationships?” and, second, to mark
the relationships as true/false. Despite only being an approximation to
relationship importance, the ranking list still proved far more difficult for
the humanists to generate than the true/false list.
We wanted to choose the statistical method that created lists most closely
correlated to the humanists’ list, as measured by Spearman correlation. The
Spearman correlations of each method were extremely similar in the humanists’
ranked lists and – combined with humanists’ concerns over producing the list in
the first place – led us to abandon the effort to optimize our algorithm for the
order of ranks. Instead, we attempted to determine which method obtained more
correct relationships – that is, relationships humanists marked as true – in the
top k estimated connections. For analysis of James
Harrington’s thirty connections, all three methods performed similarly; for John
Milton’s eighty connections, using simply the correlation coefficient led to
worse estimates earlier on, confirming that the Poisson Graphical Lasso can more
accurately reproduce sections of the network than correlation alone.
Lastly, for our third validation step, we wanted to evaluate the accuracy of our
final inferred network, in comparison to the relational knowledge conveyed by a
humanist reading of the ODNB. We therefore chose twelve people from the network
and calculated the precision and recall rates for their relationships. The
twelve people were not a random sample. Rather, they were chosen to represent a
variety of conditions within our dataset, including gender, number of estimated
relationships, deduplicated names, and appearance within individual vs. shared
ODNB biographies. Some of these conditions are relatively rare within the
dataset on the whole. For each person, we checked their inferred edges from
40-100% confidence – qualitatively tagged as our “possible” to
“certain” confidence interval – against a list of associations manually
compiled from the ODNB documents by reading through each person’s biographical
entry and other entries in which their name appears.
Together, these twelve people had twenty-eight relationships in our
likely-to-certain (60-100) confidence interval, of which three were incorrect,
leading to an 89.29% precision rate (see Figure 5). Expanding our confidence
interval to also include possible relationships (40-100) – in other words,
sacrificing precision to increase recall – gave us one hundred and seven
relationships of which twenty-seven were incorrect, leading to a
still-respectable 74.77% precision rate. The majority of these false positives
were caused by specific conditions within our data: group biographies, duplicate
names, and an abnormally high percentage of co-mentions within related
biographies. Removing the four people who satisfied these specific conditions
from our sample left us with fifty relationships and a 86.00% precision rate in
our 40-100 confidence interval, which suggests that many of the errors in our
dataset are associated with people who fulfill these conditions, which impaired
our algorithm’s ability to correctly capture their relationships via
co-mentions. Because our validation sample had taken care to include some of our
most problematic case-types, even though instances of some of those case-types
are relatively few, we deemed these measures of precision adequate as a starting
point for further curation of the network via crowd-sourcing on our website at
www.sixdegreesoffrancisbacon.com.
| Confidence Interval |
Number of SDFB Inferred Relationships |
Precision
(# correct / # found) |
Article Recall
(# found in article / # in article) |
SDFB Recall
(# found in article also in SDFB / # from
article) |
| 80-100 (certain) |
5 |
80.00% |
1.98% |
3.96% |
| 60-100 (likely) |
28 |
89.29% |
8.42% |
16.83% |
| 40-100 (possible) |
107 |
74.77% |
25.74% |
51.49% |
10-100
(unlikely) |
283 |
≥28.27%[4] |
33.66% |
67.33% |
Table 4.
Precision and Recall for a Subset of the Inferred Network
Calculating a global recall – the fraction of desired results obtained from the
ODNB as a whole – on our dataset would have required us to identify connections
across the entire biographical corpus of the ODNB, a prohibitively
labor-intensive process when done manually. We therefore calculated two partial
measures of recall instead. The first measure is article-level recall – that is,
a measure of the ability of our network to capture the same relationships as a
human reading a specific biographical article. By this measure, our recall
numbers were low, with our 40-100 confidence interval including only 25.74% of
the relationships mentioned in the article. Low article recall can be
attributed, at least in part, to two factors: first, the decision to impose a
five-mentions threshold during the NER stage, which excludes infrequently
mentioned names about which the ODNB provides insufficient network data, and,
second, the way some names are mentioned in the ODNB, which prevented them from
being picked up by NER.
Next, we calculated the measure we call “SDFB” recall – that is, the ability
of our computer algorithms to infer relationships for the subset of people
mentioned in a specific biographical article who were also included in our
overall network. This adjustment – excluding people who did not pass the
five-mentions threshold or were not captured by NER – leads to a significantly
higher recall numbers, at 51.49%, again for the 40-100 confidence interval.
Further expansion of the confidence interval to 10-100 increases the SDFB recall
rate to 67.33%, showing that within the subset of names captured by NER and
included in our node dataset, high recall rates can be achieved at the lowest
confidence intervals. Though higher recall rates would of course be desirable in
theory, we deemed it preferable to have a relatively accurate but sparse network
rather than a full but error-ridden network, and further increases in recall
would require corresponding trade-offs in precision.
5. Humanities Significance
Though the map of the early modern social network created by our inference
procedures is far from perfect, it provides a sizeable base of persons and
relationships that can be gradually corrected and expanded to encompass the
interests of a wide range of humanist scholars. This network can also be
examined, validated, refined, and expanded by scholars, students, and other
end-users through a dynamic wiki front-end with sophisticated network
visualization tools. We consider such an approach complementary to several
successful approaches that focus on smaller subsets of society [
Long and So 2013]
[
Ahnert and Ahnert 2015]
[
Basu et al. 2015]
[
During 2015]. An important possible outcome of the project is the
integration, or re-integration, of disparate threads of network scholarship.
The questions humanists care most about often turn on documentary evidence of
connections, and immersion in an archive or a published collection of letters
yields qualitative knowledge of unparalleled depth and richness. Yet the
humanities would need to see massive investments in historical analysis,
palaeography, languages, and other humanistic research skills in order to
investigate anything close to the number of relationships inferred using our
model. Since little in the current funding climate suggests that such
investments are immediately forthcoming, the promises of historical network
analysis would remain unrealized in the absence of a different approach. Hence
our probabilistic network inferences, which create a workable infrastructure for
subsequent investigation. Instead of starting the process of mapping the network
from scratch, we remediate existing scholarship for further addition, expansion,
development, and correction.
The time, moreover, appears to be right. With open access research gaining
momentum, and more and more texts entering the public domain, probabilistic
text-mining approaches afford wider lenses and present new opportunities [
Elson et al. 2010]
[
Hassan et al. 2012]
[
Underwood et al. 2013]
[
Makazhanov et al. 2014]
[
Riddell 2014]
[
Smith et al. 2014]. Even as such approaches will always benefit from the
depth and precision afforded by more traditional archival analyses,
non-commercial repositories like the HathiTrust Research Center and commercial
ones (such as Google Books) represent exciting corpora for large scale
reconstruction of historical social networks. Treating the high-quality
historical scholarship as a source of unstructured data, moreover, helps us
avoid some of the pitfalls recently observed in studies based on less scholarly
data sources like Wikipedia and Freebase [
Gloor et al. 2015]
[
Schich et al. 2014]
[
Weingart 2015]. Such studies based on declared links in
non-scholarly corpora haven’t yet achieved the plausibility achieved on the
smaller scale by old-fashioned archival work and entering attested links by
hand.
At the same time, partnerships between traditional small-scale projects and
larger-scale projects like Six Degrees of Francis
Bacon offer benefits to both sides. For those studying local
networks, large, probabilistic global networks offer chances to compare and
contextualize findings from smaller groups. For those working at larger scales
and with higher cumulative levels of uncertainty and error, small networks can
function as ground truths against which to test inferences and from which
partners may improve network models.
Our approach isn’t just a new method. It yields substantive insights as well.
Applying quantitative network measures like network degree has allowed us to
identify interesting figures, such as those who have relatively high degrees but
who don’t have ODNB entries of their own. An analysis of high-degree nodes
without ODNB entries shows an intriguingly high representation of schoolmasters
and publishers. Individuals like Thomas Smelt, an ardent royalist who taught at
the Northallerton Free School in Yorkshire, and Edward Sylvester, who ran a
grammar school in Oxford, were not deemed significant enough to warrant full
biographical entries, but they are nevertheless key nodes connecting those who
were [
Otis 2014b].
It is also possible from this work to understand more about non-British people
who figure prominently the life of the nation. Scholars can learn much about
international dimensions by attending to the frequency of non-native names
appearing frequently in the ODNB. Our five-mention threshold also helps us see
gender differences in a revealing light. The cultural practice of changing one’s
surname at marriage means that women face particular obstacles meeting our
artificially-imposed five-mention threshold. In several cases, men appear in the
dataset simply because they are mentioned in association with important women –
wives, sisters, or mothers who for various reasons may not themselves appear in
the dataset. The woman referred to in the ODNB as “Audrey,
widow of Sir Francis Anderson and eldest daughter of John Boteler, Baron
Boteler of Brantfield” does not appear in the dataset whereas John
Boteler does [
Seccombe and Kelsey 2014]. Similarly, men like Thomas Bellenden
and Richard Stubbe aren’t known as historically significant, but they appear in
the dataset because their names remain consistent whereas their wives and
sisters appear by several names. In other cases, it isn’t a personal ODNB entry
that ensures a name gets included but a legal case or a much-cited will [
Otis 2014b]. Our analysis has also illustrated how inferred
networks differ based on ways of talking about people. James VI of Scotland and
James I of England name the same person, yet each name is associated with
substantially distinct social networks [
Otis 2014a].
Ultimately, our work with the ODNB has shown that processing an entire corpus of
documents and running a statistical procedure is computationally feasible with
the resources generally available to university scholars. We have also shown
that it is possible to implement a statistical approach that infers a validated
social network. While not all highest-confidence edges are among the strongest
identified by experts – and some expert-identified relationships are not near
the top edges found – there is enough overall validation on many classes of
relationships to suggest our method is viable for reconstructing historical
social networks, within a reasonable margin of error, from large textual
corpora.
This process admittedly has several shortcomings, especially from the
perspective of humanists for whom “margin of error” is a less than
reassuring phrase. Absent further research, there is no surefire way to
determine whether a given confidence estimate accurately reflects the current
state of scholarship (as represented by the ODNB) or is instead an artifact of
the bespoke model we developed. Nor are relationships in the resulting dataset
“typed” – friends and enemies remain functionally identical in our
results, though the difference of course matters decisively in real life. Proof
or other evidence about a given relationship will initially appear elusive: the
process yields few clues about where to start researching a relationship –
though our crowd-sourcing website does at least provide users links to ODNB and
JSTOR articles that mention both people in a relationship. And humanists must be
involved at every stage for validation, interpretation, de-duping, and
disambiguation. However, the end result of this process is of demonstrable use
to experts in early modern Britain and it is likely extensible to other large
corpora.
We are the first to acknowledge that our network inference procedure comes
freighted with assumptions and technical limitations that may pose obstacles to
its transferability to other social networks generated from other data sources.
Inferring a network from biographical texts requires assuming that the
co-occurrence of names in a document is a reasonable predictor of a relationship
between the named persons. Although we believe this is a reasonable and
productive assumption for ODNB texts, it is not an equally reasonable assumption
for all data sources. Network inference will be only as good as the NER on which
it depends. Differences in NER availability and accuracy for different languages
(Stanford, for example, has separate modules for Spanish, German, and Chinese),
as well as differences in naming conventions across cultures, time periods,
discourses, and biographical data may decrease its effectiveness, though NER can
be tuned for different datasets. Because the ODNB entries have been carefully
edited and checked, they are relatively error free, but projects that aim to
mine biographical reference works that exist only in uncorrected Optical
Character Recognition documents will begin with a significant level of textual
error. Those who seek to employ our procedures on other biographical data
sources should perform checks to ensure that it is inferring edges between nodes
at level of accuracy that they deem acceptable.
Conclusion
While our interest has been in reconstructing the social network of a specific
time and place – sixteenth- and seventeenth-century Britain – there are few
barriers to re-deploying our method in other historical or contemporary
societies. We used short biographical entries, but we could with minor changes
have used contemporary book prefaces, modern scholarly articles, blogs, or other
kinds of texts. All that is needed is machine-readable text in which the
co-occurrence of names is a reasonable indicator of connections between persons.
Future work on our specific project may thus involve expanding the collection of
documents used in our network. Target documents currently include the publishing
data in the English Short Title Catalog and the prefatory material in Early
English Books Online. We would also aim to incorporate datasets whose strengths
would mitigate the data’s current weaknesses, such as collections of letters
written by women or urban apprenticeship rolls.
We have also begun to expand our network through the data provided by individual
scholars via our website interface at
www.sixdegreesoffrancisbacon.com. To encourage mass integration of
other datasets, we have incorporated features into our website to allow the
tagging of nodes and the visualization of sub-networks by those tags. However,
we also have a particular interest in scholars adding citations to confirm our
statistically predicted relationships, as well enriching those relationships by
providing information about their type and timespan. Our ultimate goal is to
create a versatile and extensible network that people interested in all aspects
of early modern Britain – including the scholarship on early modern Britain –
can use for their research, as well as to pioneer a general technique of
creating social networks from texts that other scholars can apply to other
periods and societies.
APPENDIX: The Poisson Graphical Lasso
Introduction
Our statistical approach follows the model of G.I. Allen and Z. Liu [
Allen and Liu 2012]. Inference of the network is based on statistical
graph learning techniques. Here we have a graph G=(V,E), where V is the set
of
p nodes and E is the set of pairwise edges. We
relate the graph to a random vector Y=(Y
1, ... ,
Y
p) by requiring that for each non-edge
(j,k)∉E, the variables Y
j and Y
k are conditionally independent given all the
remaining variables Y
∖{j,k}, where ∖{j,k} denotes
the complement V∖{j,k}. Commonly, Y=(Y
1, ... ,
Y
p) is assumed to follow a multivariate normal
distribution N
p(µ,∑), in which case pairwise
conditional independence holds if and only if ∑
jk-1=0 [
Lauritzen 1996].
In this case, inferring the graph corresponds to inferring the non-zero
elements of ∑
-1.
If we have
n independent and identically distributed
observations of Y, we can employ penalized likelihood methods, where we
place a one-norm penalty on elements of the concentration matrix. This
penalized likelihood can be maximized efficiently for large
p using a graphical lasso [
Friedman et al. 2008]. Alternatively, an approximate solution can be obtained through a
sequence of penalized regressions of each variable Y
j on the remaining variables Y
∖j=Y
∖{j}. We estimate σ
jk-1 = 0 if the estimated regression coefficients
of variable
j on
k or
k on
j are estimated to be 0
[
Meinshausen and Bühlmann 2006].
Poisson Graphical Lasso
For count data like ours the normality assumption may be inappropriate and a
modification of the above methods was developed by Allen and Liu for Poisson
graphical models, in which the relationships between nodes are defined by a
conditional Poisson distribution [
Allen and Liu 2012]. For each node:
The Poisson Markov random field implied by this relationship is not amenable
to inferring network structures, as it requires θ
jk ≤ 0 for all pairs {j,k} [
Allen and Liu 2012]. We
therefore proceed as they did by estimating the local log-linear models
and combine the implied local relationships into a network structure.
We can then view θ
ij as a measure of relationship
strength between
i and
j. In
Allen and Liu, the model is fit using the Poisson Graphical Lasso – a
penalized regression method similar to the graphical lasso [
Friedman et al. 2008], but modified for count data. A penalized
Poisson regression is done for each node
j’s counts
on the rest. That is, for each node we solve the following:
Here ϱ is a matrix of penalty parameters and ⋆ denotes component-wise
multiplication. An edge is determined to exist between nodes
j and
k if
θ̂jk > 0 and/or
θ̂kj > 0. The tuning parameter ϱ
can be the same for all elements and can be chosen, for example, by
stability selection [
Meinshausen and Bühlmann 2010]. Later we will allow
elements of the ϱ matrix to differ.
Modifications
The motivating data for Allen and Liu are the RNA-sequencing measurements
from
p genes in
n experiments;
their goal is to determine which genes are “connected” to each other in
a metabolic process [
Allen and Liu 2012]. Here we have the (noisy)
counts of
p names in
n
biographies; our goal is to determine which historical figures had
"connections" to each other in a variety of social contexts. Two modeling
considerations unique to this type of data and practical objective, which
lead us to slight modifications in method, are the variance of document
lengths and the irrelevance of negative edge estimates.
Documents in the ODNB vary greatly in length. People tend to have longer
biographies when biographers know more about them or have deemed them
historically significant. Allen and Liu note that it is important to
normalize the data to be approximately independent and identically
distributed Poisson random variables, since their model is sensitive to
deviations from this assumption [
Allen and Liu 2012]. To achieve this,
we break the longer documents into 500 word sections and count each section
as an observation. This introduces weak dependence among some observations,
but the chronological nature of the documents may lessen this effect. That
is, the people mentioned in the first section of Bacon’s biography may be
very different from those mentioned in the last section. Being mentioned in
the same section of a document may also be greater evidence of a connection
than simply being mentioned in the same document.
As a preliminary test of this method, we calculate the Spearman correlation
between lists of relationships provided by humanities scholars and
- relationships produced by simple correlation
- relationships produced by our model with document sectioning
- relationships produced by our model without document sectioning
For our test set, simple correlation fails first, while those for our model –
with and without sectioning – remain similar. Sectioning fails to improve
correlation on some historical actors, but it leads to slight improvements
in correlation for others.
Furthermore, when fitting the model, a large fraction of θ̂jk values are negative. When this
coefficient is negative, it does not make sense to estimate a resulting
edge, since negative coefficients imply a negative relationship between the
counts of name j and name k.
Because any specific person appears only in a small portion of the
documents, and is presumably related to only a small fraction of all the
people in the network, fitting this model tends to produce a large amount of
negative coefficients compared to positive coefficients.
Confidence Estimate Procedure
We want to be able to attach a confidence estimate to all edges (which can
be used to rank connections), instead of just obtaining a yes or no estimate
for each potential edge. Let the matrix C represent a symmetric confidence
matrix (where each entry Cjk = Ckj = confidence attached to edge existing between
person j and k). An informal
confidence estimate can be obtained by refitting the model many times on
random subsets of the data and computing the fraction of models in which a
specific edge is found in the model.
The method of estimating the final edge confidences is as follows:
- Sample half of the rows in the data matrix
- Fit Poisson Graphical Lasso on this data as follows:
- For each j (column), fit the model in
Equation 3, and obtain the coefficient estimates for ϱ=0.001
- Ignore any coefficient that has been estimated as negative
- Repeat steps (1) and (2) 100 times.
- Estimate the confidence of an edge between node j and k as
Note that θ̂(t)jk is the estimate for the coefficient on
the tth repetition of the model fitting in Step
2.
There are a number of methods described in the literature for selecting the
tuning parameter ϱ. When the goal is prediction of the response variable,
cross-validation is a natural choice. When the goal is network inference –
specifically, we want to know whether each edge is “in” or “out” –
stability selection can be used instead, as is done in Allen and Liu [
Meinshausen and Bühlmann 2010]
[
Allen and Liu 2012]. Of most use to humanities scholars, however, is
an organization of the current knowledge about relationships. Some scholars
may wish to explore numerous potential relationships to one actor. Ordering
the relationships correctly – in order of likelihood – is therefore more
important than determining a cutoff point and excluding all edges that do
not make the cut.
Our confidence estimates for a specific value of ϱ correspond to a single
point on the stability paths mentioned in Meinshausen and Bühlmann [
Meinshausen and Bühlmann 2010]. They note that the choice of range of ϱ to
use when computing the “stable variables” – or in this case, edges –
does not matter significantly. In our experiments with values of ϱ ranging
from 0.001 (many edges) to 100 (no edges), we also find the confidence
estimates tend to not vary too much for different reasonable values of ϱ,
where reasonable is defined as a low enough penalty such that variables are
actually added, but high enough penalty so that the algorithm converges
rapidly.
Name Disambiguation
Different people sometimes have the same names, and disambiguating them is
difficult. When name duplication only happens rarely, it may be feasible to
disambiguate manually. However, there are no less than twelve John Smith’s
and ten Archibald Campbell’s in our node set; overall nearly a thousand
names refer to multiple people. Furthermore, many of the people with these
names overlap in lifespans, including a large number of parents who gave
their own names to their children.
To process these duplicate names, we use a twofold method. First, we employ
chronological filters on all our potential relationship edges. Two people
cannot have a relationship if their lifespans did not overlap. We do,
however, allow a one-year margin of error so that posthumous children may
still have edges to their biological fathers. For people with unknown birth
and death dates, we allow a twenty-year span before and after their known
period of activity. For people for whom only a birth or a death date is
known, we allow for up to a 110-year lifespan, erring on the side of
inclusivity rather than exclusivity.
In the cases where there is chronological overlap in the lifespans of people
with duplicate names, we fall back on probabilities. If the name was
generated by NER, we evenly split the mentions among each of the people with
that name – that is, we assign them each an equal probability. However, if
our duplicates all have biographical entries, we assign each person a
probability based on the length of their biography. This serves as an
approximation of the relative frequency we expect each person to appear in
the overall ODNB, which we use to weight the mentions accordingly.
For example, Francis Walsingham, the principal secretary, has a biography
that is 30 times the length of Francis Walsingham, the Jesuit. Therefore we
argue a mention of Francis Walsingham in some other ODNB biography is 30
times more likely to refer to the former rather than the latter. To follow
this logic through, we would assign weights of 97% to the principal
secretary and 3% to the Jesuit. Yet we don’t want to obscure the
lesser-known Jesuit so thoroughly. Therefore, we cap the percentages at a
max/min of 75% and 25% so that someone with an extremely long biography
cannot dominate the probabilities completely. Thus in the period of overlap
between their two lifespans, 75% of the instances of “Francis
Walsingham” are attached to the principal secretary and 25% are
attached to the Jesuit. In practice, this does yield lower confidence
estimates and more false positives for “split-mention” nodes’
relationships, but we consider this an acceptable as a starting point for
further, manual curation.
Incorporating Humanist Knowledge
Prospectively, after enough humanists contribute their expert knowledge to
the network via our crowd-sourcing website, it will be possible to use their
contributions to refine our inference model by making local changes to the
penalty parameter. We could do this by allowing the penalty matrix, ϱ, to
vary for different relationships. If our experts confirm a relationship
between actors j and k, we set
ϱjk=ϱkj=0, which
usually ensures that θ̂jk,
θ̂kj ≠ 0. Similarly,
for a confirmed non-relationship – that two figures are not connected – we
would set ϱjk=ϱkj=∞,
ensuring θ̂jk, θ̂kj = 0. As more experts
label more potential relationships, we could continue to refine our model
iteratively. By helping us to tune the penalty parameter, the contributions
of (say) a hundred experts could help us to assess millions of relations
more accurately.
Works Cited
Ahnert and Ahnert 2014 Ahnert, Ruth, and S.E.
Ahnert. “A Community Under Attack: Protestant Letter
Networks in the Reign of Mary I.”
Leonardo 47, no. 3 (2014): 275–275.
doi:10.1162/LEON_a_00778.
Ahnert and Ahnert 2015 Ahnert, Ruth, and S.E.
Ahnert. “Protestant Letter Networks in the Reign of Mary I:
A Quantitative Approach.”
ELH 82, no. 1 (2015): 1-33.
Allen and Liu 2012 Allen, G.I. and Z. Liu. “A Log-Linear Graphical Model for Inferring Genetic Networks
from High-Throughput Sequencing Data.”
ArXiv e-prints (2012).
Bearman et al. 2002 Bearman, Peter, James Moody,
and Robert Faris. “Networks and History.”
Complexity 8, no. 1 (2002): 61–71.
doi:10.1002/cplx.10054.
Blei et al. 2003 Blei, David M., Andrew Y. Ng, and
Michael I. Jordan, “Latent Dirichlet Allocation.”
Journal of Machine Learning Research 3 (2003):
993-1022.
Bosch and Camp 2011 Bosch, A. and M. Camp. “A Link to the Past: Constructing Historical Social
Networks.” In The Proceedings of the Association
for Computational Linguistics Workshop on Computational Approaches to
Subjectivity and Sentiment Analysis (2011): 61–69.
Bosch and Camp 2012 Bosch, Antal van den and Matje
van de Camp. “The socialist network.”
Decision Support Systems 53, no. 4 (2012): 761-69.
doi:10.1016/j.dss.2012.05.031.
Campbell 2004 Campbell, Gordon. “Milton, John (1608-1674), poet and polemicist.” In
Matthew, H.C.G. and Brian Harrison (eds). Oxford Dictionary
of National Biography. Oxford University Press, Oxford (2004);
online edn, (2007).
Collini 2005 Collini, Stefan. “Our Island Story,” London Review
of Books, 27.2 (2005): 3-8.
Elson et al. 2010 Elson, David K., Nicholas Dames,
and Kathleen R. McKeown. “Extracting Social Networks from
Literary Fiction,”
Proceedings of the 48th Annual Meeting of the Association
for Computational Linguistics (2010): 138-147.
https://www.aclweb.org/anthology/P/P10/P10-1015.pdf Evans 2011 Evans, James A. and Jacob G. Goster.
“Metaknowledge,”
Science, 331.6018 (2011): 721-725.
Finkel et al. 2005 Finkel, J.R., T. Grenager, and
C. Manning. “Incorporating Non-local Information into
Information Extraction Systems by Gibbs Sampling.” In
Proceedings of the 43rd Annual Meeting of the Association for
Computational Linguistics (2005): 363-370.
http://nlp.standford.edu/manning/papers/gibbscrf3.pdf Friedman et al. 2008 Friedman, J., T. Hastie,
and R. Tibshirani. “Sparse inverse covariance estimation
with the graphical lasso.”
Biostatistics 9 (2008): 432-441.
Gloor et al. 2015 Gloor, Peter, Patrick De Boer,
Wei Lo, Stefan Wagner, Keiichi Nemoto, and Hauke Fuehres. “Cultural Anthropology Through the Lens of Wikipedia - A Comparison of
Historical Leadership Networks in the English, Chinese, Japanese and German
Wikipedia.” arXiv:1502.05256 [cs], February 18, 2015.
http://arxiv.org/abs/1502.05256.
Glymour et al. 2001 Glymour, Clark, Richard
Scheines, and Peter Spirtes. Causation, Prediction, and
Search, 2nd Ed. MIT Press, Cambridge Mass. (2001).
Goldfarb et al. 2013 Goldfarb, Doron, Max
Arends, Josef Froschauer, and Dieter Merkl. “Comparing Art
Historical Networks.”
Leonardo 46, no. 3 (2013): 279–279.
doi:10.1162/LEON_a_00575.
Hassan et al. 2012 Hassan, Ahmed, Amjad Abu-Jbara,
and Dragomir Radev, “Extracting Signed Social Networks From
Text.”
Proceedings of the TextGraphs-7 Workshop (2012):
6-14.
http://www.aclweb.org/anthology/W12-4102 Lauritzen 1996 Lauritzen, S.L. Graphical Models. Oxford Statistical Science Series
17. The Clarendon Press Oxford University Press, New York (1996).
Long and So 2013 Long, Hoyt, and Richard So. “Network Science and Literary History.”
Leonardo 46, no. 3 (2013): 274–274.
doi:10.1162/LEON_a_00570.
Makazhanov et al. 2014 Makazhanov, Aibek,
Denilson Barbosa, and Grzegorz Kondrak. “Extracting Family
Relationship Networks from Novels.” arXiv:1405.0603 [cs.CL].
Matthew and Harrison 2004 Matthew, H.C.G. and
Brian Harrison (eds). Oxford Dictionary of National
Biography. Oxford University Press, Oxford (2004); online edn,
(2007).
McGann 2014 McGann, Jerome. A
New Republic of Letters: Memory and Scholarship in the Age of Digital
Reproduction. Cambridge, Massachusetts: Harvard University Press,
2014.
McPherson, Smith-Love and Cook 2001 McPherson,
Miller, Lynn Smith-Lovin and James M. Cook. “Birds of a
Feather: Homophily in Social Networks.”
Annual Review of Sociology 27 (2001):
415-444.
Meeks and Weingart 2012 Elijah Meeks and Scott
Weingart, eds., Journal of Digital Humanities 2.1
(2012), “Topic Modeling” special issue.
Meinshausen and Bühlmann 2006 Meinshausen, N.
and P. Bühlmann. “High-dimensional graphs and variable
selection with the lasso.”
Annals of Statistics 34 (2006): 1436-1462.
Meinshausen and Bühlmann 2010 Meinshausen, N.
and P. Bühlmann. “Stability selection.”
Journal of the Royal Statistical Society: Series B
(Statistical Methodology) 72 (2010): 417-473.
Moretti 2011 Moretti, Franco. “Network Theory, Plot Analysis.”
New Left Review 68 (2011): 80–102.
Otis 2014a Otis, Jessica. “What’s in a Name? The Many Nodes of King James VI and I.”
Six Degrees of Francis Bacon: Reassembling the Early Modern
Social Network, Sept. 16, 2014.
http://6dfb.tumblr.com/post/97645842306/ Peltonen 2004 Peltonen, Markku. “Bacon, Francis, Viscount St Alban (1561-1626), lord
chancellor, politician, and philosopher”. In Matthew, H.C.G. and
Brian Harrison (eds). Oxford Dictionary of National
Biography. Oxford University Press, Oxford (2004); online edn,
(2007).
Porter 1980 Porter, M.F. “An
algorithm for suffix stripping.”
Program, 14(3) (1980): 130−137.
Riddell 2014 Riddell, A. “How
to Read 22,198 Journal Articles: Studying the History of German Studies with
Topic Models.” In Distant Readings: Topologies
of German Culture in the Long Nineteenth Century, edited by Matt
Erlin and Lynne Tatlock, 91--114. Rochester, New York: Camden House,
2014.
Schich et al. 2014 Schich, Maximilian, Chaoming
Song, Yong-Yeol Ahn, Alexander Mirsky, Mauro Martino, Albert-László Barabási,
and Dirk Helbing. “A Network Framework of Cultural
History.”
Science 345, no. 6196 (August 1, 2014): 558–62.
doi:10.1126/science.1240064.
Seccombe and Kelsey 2014 Seccombe, Thomas and
Sean Kelsey. “Leigh, Francis, first earl of Chichester (d.
1653), politician and courtier”. In Matthew, H.C.G. and Brian
Harrison (eds). Oxford Dictionary of National
Biography. Oxford University Press, Oxford (2004); online edn,
(2007).
Simmel 1950 Simmel, Georg. The Sociology of Georg Simmel. Translated by Kurt H. Wolff. Simon
and Schuster, 1950.
Smith et al. 2014 Smith, D.A., R. Cordell, E.M.
Dillon, N. Stramp, and J. Wilkerson. “Detecting and Modeling
Local Text Reuse.” In 2014 IEEE/ACM Joint
Conference on Digital Libraries (JCDL), 183–92, 2014.
doi:10.1109/JCDL.2014.6970166.
Underwood et al. 2013 Underwood, Ted, Michael
L. Black, Loretta Auvil, and Boris Capitanu. “Mapping
Mutable Genres in Structurally Complex Volumes.”
arXiv:1309.3323 [cs], September 12, 2013.
http://arxiv.org/abs/1309.3323.