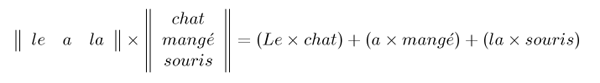DHQ: Digital Humanities Quarterly
2007
Volume 1 Number 1
2007 1.1  |  XML |  PDF |  Print

Reading Potential: The Oulipo and the Meaning of Algorithms

Mark Wolff  <wolffm0_at_hartwick_dot_edu>, Hartwick College

Abstract

Recent efforts to reconceptualize text analysis with computers in order to broaden the appeal of humanities computing have invoked the example of the Oulipo. Although there are similarities between the activities of the Oulipo and the new approach to computer-assisted literary analysis, the development of tools for the express purpose of encouraging scholars to play with texts does not follow the model of Oulipian research into potentialities. For the Oulipo, potential text analysis is less a question of interpreting literature than of supplying algorithms for the good use one can make of reading. Producing exemplary interpretations with algorithms is a secondary consideration. Oulipian constraints are better understood as toys with no intended purpose rather than as tools we use with some objective in mind. The procedures for making sense of texts provide for their own interpretation: they are not only instruments for discovering meaning but also reflections on making meaning.

1
Researchers in the humanities who focus their efforts on the use of computer technology to engage texts have wrestled with the relevance of their work. Within the field of humanities computing, scholars have used information technology to analyze single texts as well as large corpora in search of patterns that would be difficult to detect without the use of machines. Despite the ability of computers to organize and process massive amounts of textual data, the broader community of literary scholars has not readily accepted the potential of digital technology in humanities research. In 1993, Mark Olsen argued that scholars using computers to analyze texts tended to focus on quantifying a literary effect instead of exploring how texts are meaningful in broader historical and cultural contexts [Olsen 1993]. Recent efforts to reconceptualize text analysis with computers have emphasized hypothesis testing and the search for elusive patterns that may provide insight into interpreting texts. In order to broaden the appeal of this new direction in humanities computing, advocates have invoked the example of the Oulipo, a group of writers in France that invent “potential” ways to create literature using rigorous formal constraints. The idea that computers can lend themselves to formal methods of subjective textual study (thereby assuaging concerns that computers will make reading literature a soulless process of crunching numbers) is expressed forcefully by Jerome McGann in his book Radiant Textuality. For McGann, the Oulipo set an example of what can be done with combinatorial methods to realize Alfred Jarry's program of pataphysics as a “science of exceptions”  [McGann 2001a, 222]. Rejecting the practice of using computers as tools for objective, empirical research, Stephen Ramsay envisions an algorithmic criticism that transforms texts “for the purpose of releasing what the Oulipians would call their ‘potentialities’ ”  [Ramsay 2003, 172]. Stéfan Sinclair has developed HyperPo as a web-based tool for helping scholars read and play with texts using procedures inspired by the Oulipo [Sinclair 2003]. The idea of playing with texts using computers is pursued further by Geoffrey Rockwell who calls for the creation of web-based playpens where scholars can experiment with tools and discover new ways to formulate and test hypotheses about what texts mean [Rockwell 2003].
2
Although there are similarities between the activities of the Oulipo and the new approach to computer-assisted literary analysis, the development of tools for the express purpose of encouraging scholars to play with texts does not follow the model of Oulipian research into potentialities. For the Oulipo, the invention of procedures for playing with texts is its own end, an intellectual activity that invites application but does not require adoption by others as an indication of success. According to Raymond Queneau, one of the founding members of the Oulipo, “The word ‘potential’ concerns the very nature of literature; that is, fundamentally it's less a question of literature strictly speaking than of supplying forms for the good use one can make of literature. We call potential literature the search for new forms and structures that may be used by writers in any way they see fit”  [Motte 1986, 38]. Queneau makes it clear that what the Oulipo does relates to but does not constitute literary creation. Writing is a derivative activity: the Oulipo pursue what we might call speculative or theoretical literature and leave the application of the constraints to practitioners who may (or may not) find their procedures useful. According to François Le Lionnais, another founding member, a method for writing literature need not produce an actual text: “method is sufficient in and of itself. There are methods without textual examples. An example is an additional pleasure for the author and the reader”  [Bens 1980, 88].
3
The Oulipo did not articulate a clear statement explaining potential methods for reading literature, but we can extrapolate a definition from how they described their efforts to invent methods for writing literature. Potential text analysis is less a question of interpreting literature than of supplying algorithms for the good use one can make of reading. Producing exemplary interpretations with algorithms is a secondary consideration. It follows that the interpretation of texts using a computer should not be in and of itself the objective of potential text analysis. The objective should be the invention of algorithms that scholars may (or may not) use, according to their own interests. The potentiality of computers as tools for text analysis implies that scholars engaged in the derivative activity of interpreting literature may not find such methods useful.
4
By inventing procedures for generating texts, the Oulipo separated the formal aspects of writing from its content so that procedures for making texts could be carried out independently of those who invent the procedures. As the Oulipo declared in a presentation of its work to the Collège de 'Pataphysique, this is a new era in the history of literature: “Thus, the time of created creations, which was that of the literary works we know, should cede to the era of creating creations, capable of developing from themselves and beyond themselves, in a manner at once predictable and inexhaustibly unforeseen”  [Motte 1986, 48–49]. The transition from created creations to creating creations divides the traditional author function into what Christelle Reggiani identifies as the biphasic Oulipian functions of the inventor and the poet [Reggiani 1999, 110]. The first phase involves an inventor who devises constraints that will guide the production of a text. The inventor does not worry about what the constraints will produce: he seeks consistency and robustness in formal procedures. During the second phase, a poet applies the constraints in a particular instance and produces a text. Clearly the role of the inventor is privileged over the poet. Whereas the poet can only follow the rules of literary form and assemble a finite number of texts, the inventor explores potential forms which can generate innumerable texts.
5
When the Oulipo formed in 1960, one of the first things they discussed was using computers to read and write literature. They communicated regularly with Dmitri Starynkevitch, a computer programmer who helped develop the IBM SEA CAB 500 computer. The relatively small size and low cost of the SEA CAB 500 along with its high-level programming language PAF (Programmation Automatique des Formules) provided the Oulipo with a precursor to the personal computer [Starynkevitch 1990]. Starynkevitch used the machine to create an imaginary telephone directory composed of realistic names and numbers generated by his computer:
  • Tab Philippe, 14, rue de La Machine normande
  • Dubit Anatole, 20, av. du Moine Romain
  • Pouguinf Jules, 45, rue de la Maison
  • Herebier Adolphe, 38, rue des Maisons Jolies
  • Lir Yves, 64, rue Saint-Pierre
  • Lorbont Edouard, 21, av. du Buisson Gai
  • Sech André, 18, rue des Montagnes riveraines
  • Dreber Gilbert, 5, rue Jules Marcel
  • Micier Michel, 54, rue Saint Augustin
  • Debate Robert, 25, rue des Montagnes
  • Locrobelier Adolphe, 18, av. des Gares étroites
  • Rexer Augustin, 1, rue de la Tour blonde
  • Quimier Anatole, 20, rue du Buisson galant
Example 1. 
Computer-generated names and addresses from Starynkevitch's telephone directory
The algorithms Starynkevitch used were based mainly on random number generators. Given names and street names were selected from a predetermined list. Surnames were composed from sets of letter sequences that alternated between open and closed syllables [Bens 1980, 162–163]. The Oulipo was impressed with the mock phone book but Queneau did not believe the computer application had “potential”. Le Lionnais found the phone book interesting because it was not particularly interesting: it was neither bizarre nor funny, and it looked like a real phone book. What worried the Oulipo was the aleatory nature of computer-assisted artistic creation: they sought to avoid chance and automatisms over which the computer user had no control [Bens 1980, 157–8].
6
In 1981 the Oulipo published Atlas de littérature potential where they described some of the computer applications they had devised for reading literature. Their early experiments included machine-assisted readings of Queneau's Cent mille milliards de poèmes. In this deceptively small book, Queneau had composed ten sonnets in such a way that the reader could select the first line of any sonnet, the second line of any sonnet, etc., and generate one of 1014 possible sonnets. The book itself contains the mechanism for generating poems: each line is printed on a strip of paper, and the reader can select strips from the original sonnets to generate a potential sonnet [Queneau 1961]. Dimitri Starynkevitch had programmed his SEA CAB 500 machine to compose sonnets from Queneau's Cent mille milliards de poèmes. 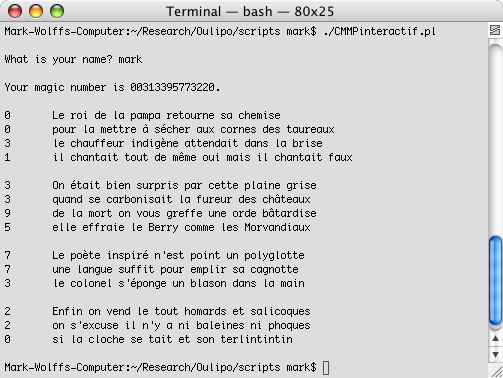In 1975 the Atelier de Recherches et Techniques Avancées, or ARTA, wrote a computer program that produced instantiations of the Cent mille milliards de poèmes as a function of a user's name and the time it took him or her to type it. It is not difficult to simulate ARTA's computer program to produce poems from Queneau's original text by counting the number of seconds it takes a user to type his or her name and using that information to calculate a “magic number”:
Screenshot of command-line program running in a terminal
Figure 1. 
A simulation of ARTA's program for generating poems from Queneau's Cent Mille Milliards de Poèmes. In English (translation by Beverly Charles Rowe at http://www.bevrowe.info/Poems/QueneauRandom.htm; the reader can select specific lines from the original 10 sonnets to reproduce any of the 100,000,000,000,000 potential poems) it reads as follows:
The pampas king betrays his devotees
and decks the bulls that roam the paramo
the native driver's waiting in the breeze
the re in in [sic] all his songs came out as doh
You'll view so plain a plain with trembling knees
as castles blaze and palaces burn low
for death casts piles of shit on pedigrees
it's scary both for hick and aristo
The impassioned poet isn't polyglot
one language in his brain that's all he's got
shame gives the colonel's brow a greasy sheen
All's sold the prawns the lobsters our whole stock
say sorry that no whales came back to dock
unless the bell is silent and serene
Each digit in the magic number corresponds to a verse from one of the original ten sonnets. The program's algorithm provides a certain degree of interaction between the user and the machine, and the results of running the program are theoretically reproducible if a user types the same name in the same amount of time. The algorithm therefore has potential, but only insofar that it accelerates the production of poems. It may be easier and more entertaining to generate poems automatically without relying on user input, and there are several web sites on the Internet that do this. One could even use a random number function:
Screenshot of command-line program running in a terminal
Figure 2. 
A program for generating poems from Queneau's Cent Mille Milliards de Poèmes using a random number function. In English (translation by Beverly Charles Rowe, http://www.bevrowe.info/Poems/QueneauRandom.htm) it reads as follows:
The Parthenon horse looks nervous on the frieze
being twinned is better far than single-o
the chosen fruit is hued a bright cerise
all during Lent one fruit's the ratio
The Papuan sucks his friend's apophyses
as castles blaze and palaces burn low
the flanks protected by chevaux de frise
it's scary both for hick and aristo
The clever students may have lost the plot
to cease from scratching parchment he cannot
the motorway laps up leaked gasoline
Those transalpine relations interlock?
you cannot number off each ploch and pock
true twinship blames whatever's in the gene
Such a program has no potential in the Oulipian sense because random numbers produce aleatory effects. The original algorithm preserves an active role for the user, even if that role requires the minimal engagement of typing one's name in order to sustain the creative process.
1
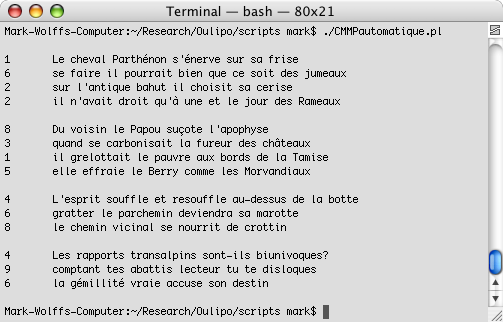
Paul Braffort and Jacques Roubaud, two Oulipians with backgrounds in mathematics and computer science, formed the Atelier de Littérature Assistée par la Mathématique et les Ordinateurs (ALAMO) in 1980 to explore computer-assisted writing. Following the model of Queneau's Cent mille milliards de poèmes, the ALAMO wrote computer programs to produce texts according to the rules of various genres, such as poems and aphorisms. Braffort explained that combinatorial methods for generating texts with computers fall into two categories. 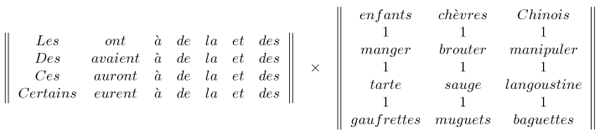The first category, applicational methods, involves templates for arranging words according to their grammatical function. One particularly amusing application generates what the ALAMO calls “Rimbaudelaires”, poems based on the structure of Rimbaud's poem “Le Dormeur du Val” and composed of vocabulary from Baudelaire's works:
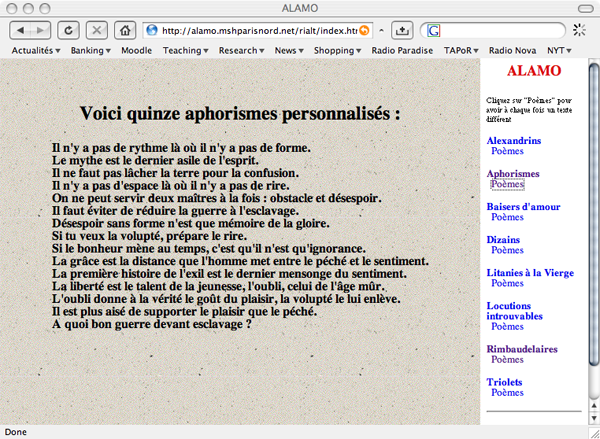
Screenshot of web page
Figure 3. 
Sample Rimbaudelaire poem from the ALAMO's web site (http://alamo.mshparisnord.net/rialt/index.html). Here is a translation (mine):
There is a countryside king where a shadow flower rolls
Simply hanging in the shadows pâtés
Of love; where the regret of dark memory
Drinks: it is a former happiness that shines sideways.
A noble demon, hatred dark and size black,
His tongue bathing in the ginger-white ravine,
Rains; he leans in the shade, under the lustrous fabric,
Noble in his cold dale where the chest speaks falsely.
The heavens in desires, it rains. This frail bird
Would slide a wary shark, he flees the hail:
Medallion, love him tenderly: he is great.
The sweet liquors do not make his nostril stomp;
It rains in the bell, the sea on his chest,
Wary. He has noble skies in the slow gladiolus.
Another example is Marcel Bénabou's method for generating aphorisms [Bénabou 1980]. Braffort developed a program that operationalized Bénabou's algorithm by abstracting the structures common to adages and substituting new terms into the structures:
Screenshot of web page
Figure 4. 
Sample aphorisms from the ALAMO's web site (http://alamo.mshparisnord.net/rialt/index.html). Here is a translation (mine):
There is no rhythm where there is no form.
Myth is the final sanctuary of the mind.
One must not let go of the earth for confusion.
There is no space where there is no laughter.
One cannot serve two masters at once: obstacle and despair.
One must avoid reducing war to slavery.
Despair without form is only memory of glory.
If you want sensuality, prepare for laughter.
If happiness leads to time, it's because happiness is only ignorance.
Grace is the distance man places between sin and feeling.
Freedom is the gift of youth, oblivion the gift of age.
Oblivion gives truth the taste of pleasure and sensuality takes it away.
It is easier to tolerate pleasure than sin.
What good is war before slavery?
The potential of these computer programs resides in the way fragments of words and verses are recombined according to a set of well-defined rules. Poetic forms can thus be understood as algorithms for creating meaning with language.[1] The ALAMO devised ways to formalize poetics in order for a computer to generate structured texts which may or may not make sense. The actual poems produced by the programs are derivatives of the way computers can be harnessed to explore language. Reading these computer-generated texts can be amusing because of unexpected or incongruous combinations of words that oddly make sense. Despite their uncanny effects, however, texts produced through applicational methods still bear the mark of the inventor who not only determines the templates into which syntagma are inserted but also the stock of words and phrases from which the computer program draws.
1
The second category, implicational methods, involves further abstraction of structures. Instead of creating templates for arranging words according to predetermined syntactic and semantic categories, the inventor devises rules for making templates. According to Braffort, “implicational methods take a further step [in the direction of invention]. The very logic of the text is controlled by the program: a global syntagma comes into play and becomes manifest as a supervisor of local syntagmas”  [Braffort 1984, 18]. The logic of implicational methods relies on recursion in programs that generate texts, allowing for systematic processing of linguistic elements below the level of the “master” program. With recursion, computer programs can continuously refine their output in ways the inventor would not be able to easily predict. Implicational methods provide computers with a small measure of independence. Braffort and the other members of the ALAMO developed a number of formal systems for expressing the relationships between linguistic elements in literary texts. One of these systems, FASTL (Formalismes pour l'Analyse et la Synthèse de Textes Littéraires), used recursion and iteration to encompass all forms of written communication. It is no accident that, with Braffort a computer scientist and Roubaud a mathematician, FASTL resembles abstract systems of representation used in the sciences: “USFAL [‘Un Système Formel pour l'Algorithmique Linguistique’, a precursor to FASTL] will be for theoretical literature what mathematical disciplines such as the theory of differential equations can be for physics, economics, etc.”  [Oulipo 1981, 128]. An important feature of FASTL is its scalability in representing textual elements. Text objects are organized within a hierarchy that extends from the characters on a page or screen to entire libraries or corpora. Expressions for representing relationships between objects at one level of the hierarchy should be applicable to relationships of objects at another level within the hierarchy. Algorithms for analyzing texts can potentially operate recursively:

For the mind of a mathematician, we will say that the algorithm is a function that, when applied to [a given text] considered as its argument provides a result. This result is itself a text, but a text with a complex organization that is highly structured with fragments of symbolic texts and readings [...]  (Oulipo 1981, 133, author's emphasis.)

Given the scalability of FASTL and the possibility of recursion, abstract representations of texts within FASTL could potentially undergo further processing and abstraction. The complexity of texts as hierarchically structured objects, however, makes devising an algorithm that operates from the level of the word to that of the sentence, paragraph and chapter extremely difficult. Nevertheless, the ALAMO's research into computer-assisted text analysis envisioned the possibility of computational mise en abîme where the results of analysis can repeatedly feed as textual arguments into algorithmic functions in a theoretically never-ending process. The Oulipo anticipated the potentiality of recursion early in its history: in a report submitted to the Collège de Pataphysique (an institution dedicated to the pursuit of the “the science of exceptions”), the group proclaimed that computers would make possible the

abstracting [of] commonplaces from the structures of commonplaces — and then a “squared” topology of these places, and so forth until one attains, in a rigorous analysis of this regressus itself, the absolute, the Absolute “whose armature,” according to Jarry, “is made of clichés.”  [Motte 1986, 50]

The efforts of the ALAMO to develop computer applications that generate texts through recursion have met limited success, however [Braffort 2006].
2
As Braffort himself recognized, implicational methods for writing texts with machines are related to research in artificial intelligence. The Oulipo does not seek to replace the human writer who is at the center of the Oulipian enterprise. The group's approach to automating potential literature follows the Cartesian method of dividing a complicated question (how does writing occur?) into smaller questions that are easier to solve. Recursion is one technique that could allow humans to pursue new forms of writing by handing off some of the work to machines. But where is the limit to recursion? In 1963 Jacques Duchateau argued that what interests the the Oulipo most in machines is their capacity for organizing information:

organized means that data will be processed, that all the possibilities of the data will be examined systematically according to a model that will be furnished eventually by man or another machine, the model of which will also be furnished by a third machine, the model of which, etc.  (in Bens 1980, 251)

Duchateau attempts to allay fears of an unintended determinism resulting from the aleatory effects of rigorous textual constraints, but his notion of organization does not make any distinction between humans and machines as information processing units. His definition of organization is recursive: it holds that a machine processes information according to a model based on another machine, which in turn processes information according to the model of another machine, etc. We might be tempted to think that for the Oulipo, humans are the first machines after which all other machines are modeled, but Duchateau's definition places humans and machines on the same ontological footing. Ultimately there is no central processing unit which controls all the subprocesses. The Oulipian inventor may create blueprints for literature, but he distances himself from the work of applying rules and crafting texts. Despite his privileged isolation from the particularities of writing, the inventor is just another process that communicates with other processes.
3
If, as Duchateau explains it, the process of writing literature with machines consists of organizing information in new ways to analyze and synthesize texts, traditional authorship will eventually give way to a set of increasingly anonymous and autonomous processes. During one of its reunions in the early 1960s the Oulipo anticipated the risk of automatism in the structures they were defining. The group attempted to make room for individual freedom but they were unable to reconcile freedom with automatism. Jacques Bens recognized that every structure automatized writing to a certain extent, and Claude Berge added that potential literature generated new automatisms [Bens 1980, 144]. Le Lionnais insisted that a sufficiently complex system of constraints offered writers a number of options from which they could choose. The Oulipians wanted to avoid the unconscious automatisms of the Surrealists, but the conscious use of structures in their writing produced what they could not avoid describing as “automatic”. Le Lionnais admitted that “it is true that the birth of machines has modified the current sense of the word ‘automatic’ ”  [Bens 1980, 185]. The Oulipo recognized that the problem of using computers to create texts stemmed from the writer's inability to remain aware of how the machine applied constraints. In the 1970s the Oulipo introduced the notion of the clinamen, which helped to resolve this dilemma. Based on a conception of the movement of atoms in Lucretius' On the Nature of Things, the clinamen is the primordial anti-constraint: it makes creation possible by introducing chance and spontaneity in an ordered universe [Motte 1986]. The Oulipo recovered a sense of the unexpected in the constraints they used but they wanted to define and control how chance would play in their writing. An algorithm is productive as a tool for engaging texts as long as the user can follow how the algorithm works and anticipate the effects of chance. If the computational system becomes too complex or too unpredictable, the act of interpretation will depend on opaque sequences of data processing of which the user must remain unconscious.
4
The Oulipians developed at least two algorithms for reading texts. The first is Harry Mathews's Algorithm, which consists of combinatoric operations over a set of structurally similar but thematically heterogeneous texts. These operations generalize the structure of the Cent mille milliards de poèmes and allow for the production of new texts. For instance, given four texts each consisting of nine elements
1. a1 b1 c1 d1 e1 f1 g1 h1 i1
2. a2 b2 c2 d2 e2 f2 g2 h2 i2
3. a3 b3 c3 d3 e3 f3 g3 h3 i3
4. a4 b4 c4 d4 e4 f4 g4 h4 i4
Table 1. 
Before applying Mathews's Algorithm
we can use Mathews's Algorithm to produce four new combinations:
1. a1 b2 c3 d4 e1 f2 g3 h4 i1
2. a4 b1 c2 d3 e4 f1 g2 h3 i4
3. a3 b4 c1 d2 e3 f4 g1 h2 i3
4. a2 b3 c4 d1 e2 f3 g4 h1 i2
Table 2. 
After applying Mathews's Algorithm
5
In his Exercices de style, Queneau relates the same banal incident on the Paris bus system ninety-nine times, each instance demonstrating a particular textual style. By identifying a nine-part structure common to four of the exercises, one can apply Mathews's Algorithm to generate four new versions of the incident (see http://bumppo.hartwick.edu/Oulipo/Exercices.html). According to Mathews, the the aim of the algorithm “is not to liberate potentiality but to coerce it”  [Motte 1986, 139]. A “new” reading of a text (or a reading of a “new” text) through the algorithm is not the objective. The use of the algorithm is meaningful in that the apparent unity of texts can be dismantled and give way to a multiplicity of meanings. Mathews invented a system of constraints that illustrates what poststructuralists have maintained for decades.[2]
6
The second example is Raymond Queneau's matrix analysis of language, published in Etudes de linguistique appliquée and discussed at length during one of the Oulipo's early gatherings. Using principles of linear algebra, Queneau devised a mathematics of the French language that describes the construction of word groups. 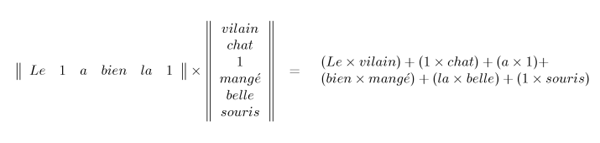He began by dividing all elements of speech into two categories: signifiers, which include nouns, adjectives, and verbs (except avoir and être); and formatives, which include everything else (avoir, être, pronouns, articles, conjunctions, prepositions, adverbs, interjections, etc.). Given a word group such as a sentence, one can construct two matrices where the first matrix contains all formatives and the second all signifiers.
Image of mathematical notation
Figure 5. 
Queneau's language matrices: A single sentence represented as a product of two matrices. (The × cat) + (has × eaten) + (the × mouse).
If a word group contains two consecutive formatives or signifiers, one can use a unitary element in order to construct the matrices.
Image of mathematical notation
Figure 6. 
The unitary element permits the representation of word groups with consecutive formatives or signifiers. (The × naughty) + (1 × cat) + (has × 1) + (thoroughly × eaten) + (the × beautiful) + (1 × mouse).
The product of a formative and a signifier is a bi-word. By adopting the conventions that neither (1 × 1) nor (Y × 1) + (1 × Z) are allowed, one avoids uninteresting or redundant bi-words. Where Y and Z are any formative and signifier respectively, we can designate (Y × Z) as B, (Y × 1) as F and (1 × Z) as S. This gives us BBB for Figure 5 and BSFBBS for Figure 6.
7
Queneau himself constructed matrices for a number of short sample texts, but his ability to apply the algorithm to lengthy texts was limited because he did his calculations manually. With the availability of part-of-speech taggers such as Helmut Schmid's TreeTagger, it is relatively easy to perform a matrix analysis of any text written in French with a computer [Schmid 2006]. [3] Consider the following representation of the first paragraphs of Flaubert's Madame Bovary:
  • [Nous 1][étions 1][à 1][l' Etude][ ,][quand 1][le Proviseur][1 entra]
  • [1 suivi][d' 1][un nouveau][1 habillé][en bourgeois][et 1][d' 1]
  • [un garçon][de classe][qui portait][un grand][1 pupitre][ .][Ceux 1]
  • [qui dormaient][1 se][1 réveillèrent][ ,][et 1][chacun 1][se leva]
  • [comme surpris][dans 1][son travail.][Le Proviseur][nous fit][1 signe]
  • [de 1][nous rasseoir][ ;][puis 1][ ,][se tournant][vers 1][le maître]
  • [d' études][1 :][ -][1 Monsieur][1 Roger][ ,][lui dit][-il 1][à 1]
  • [demi-voix 1][ ,][voici 1][un élève][que 1][je 1][vous recommande][ ,]
  • [1 il][entre 1][en cinquième][ .][Si 1][son travail][et 1][sa conduite]
  • [sont méritoires][ ,][il passera][dans les][1 grands][ ,][où 1][l' appelle]
  • [son âge.][1 Resté][dans 1][l' angle][ ,][derrière 1][la porte][ ,][si 1]
  • [bien 1][qu' 1][on 1][l' apercevait][à peine][ ,][le nouveau][était 1]
  • [un gars][de 1][la campagne][ ,][d' 1][une quinzaine][d' années][environ 1]
  • [ ,][et 1][plus 1][haut 1][de taille][qu' 1][aucun 1][de 1][nous tous][ .][Il 1]
  • [avait 1][les cheveux][1 coupés][1 droit][sur 1][le front][ ,][comme 1]
  • [un chantre][de village][ ,][l' air][1 raisonnable][et 1][fort embarrassé][ .]
  • [Quoiqu' 1][il 1][ne 1][fût 1][pas large][1 des][1 épaules][ ,]
  • [son habit-veste][de drap][1 vert][à boutons][1 noirs][1 devait][le gêner]
  • [aux entournures][et laissait][1 voir][ ,][par 1][la fente][des parements][ ,]
  • [des poignets][1 rouges][1 habitués][à 1][être nus.][Ses jambes][ ,][en 1]
  • [bas bleus][ ,][1 sortaient][d' 1][un pantalon][1 jaunâtre][très tiré][par 1]
  • [les bretelles.][Il 1][était chaussé][de souliers][1 forts][ ,][mal cirés][ ,]
  • [1 garnis][de clous][ .]
Example 2. 
Madame Bovary as a sequence of word pairs
The text is broken down into bracketed pairs representing bi-words, signifiers, formatives and punctuation. We can transform the text into an abstract sequence of the letters F, S and B:
FFFB, FBSSFBSBFFBBBBS. FBSS, FFBBFBBBSFB; F, BFBBS- SS, BFFF, FBFFB, SFB. FBFBB, BBS, FBBSFB, FB, FFFFBB, BFBFB, FBBF, FFFBFFFB. FFBSSFB, FBB, BSFB. FFFFBSS, BBSBSSBBBS, FBB, BSSFBB, FB, SFBSBFBFBBS, B, SB.
Example 3. 
Abstract reduction of Madame Bovary
Note that punctuation separates word groups. One can compute the probability ratios of formatives (F), signifiers (S) and bi-words (B) in a text:
F = 55 0.369127516778524
S = 28 0.187919463087248
B = 66 0.442953020134228
Table 3. 
Probabilty ratios in the passage from Madame Bovary
F + S + 2B always equals the total number of words in a text.
8
Queneau believed that matrix analysis could provide “indices of an author's style that may be interesting, for they escape the conscious control of the writer and doubtless depend on several hidden parameters”  [Queneau 1965, 319]. He did not elaborate further on how one could determine such indices, but his matrix analysis can be combined with the use of Markov chains in order to measure the authorship of texts. Given the four letters F, S, B and P to designate formatives, signifiers, bi-words and punctuation, we can construct a transition matrix of the probabilities of letter sequences in the passage from Madame Bovary:
S F B P
S 0.23809524 0.33333333 0.23809524 0.19047619
F 0.00000000 0.32727273 0.61818182 0.05454545
B 0.17391304 0.17391304 0.27536232 0.37681159
P 0.12121212 0.51515152 0.33333333 0.03030303
Table 4. 
Transition matrix of passage from Madame Bovary
9
Note that the probability of the sequence FS is zero because such a sequence would be an instance of a bi-word. Dmitri Khmelev and Fiona Tweedie have developed a technique for determining authorship using Markov chains and transition matrices for the sequence of letters in a text. Their technique can also be used with formatives, signifiers, bi-words and punctuation. Given a text of which the author is one of a group of known authors in a corpus, we can determine the probability that the text in question was written by each of the known authors. I have used this technique with a corpus of 1569 texts written by 290 authors from the ARTFL database (http://humanities.uchicago.edu/orgs/ARTFL/). I first selected randomly a text from each author in the corpus. Of the 290 randomly selected texts, 186 were correctly attributed to the authors who wrote them, or 64 percent. According to Khmelev and Tweedie, this represents an error rate of 0.153 percent. I then performed a cross-validation of the ARTFL corpus where 557 texts were correctly classified by author. These results are similar to those of Khmelev and Tweedie, suggesting that the combination of matrix analysis and Markov chains offers an interesting technique for measuring “linguistically microscopic” data to determine the authorship of texts written in French [Khmelev and Tweedie 2001, 302–4]. [4]
10
Whatever the promise of matrix analysis in providing quantitative evidence for measuring an author's style, Queneau expressed greater interest in its mathematical properties. He proved several theorems on the behavior of matrices and identitified similarities between them and the Fibonacci series [Queneau 1964]. He also explored the potentiality of matrices without basing his analyses on written texts. He and the other members of the Oulipo were intrigued by matrix analysis but looked forward to the creation of poems written in columns and rows (in Bergens 61–66):
An example of Queneau's two-dimensional matrix poems
Figure 7. 
By factoring rows from the first matrix (formatives) with columns from the second matrix (signifiers), the reader can generate 4 × 3 = 12 distinct verses:
Les enfants ont à manger de la tarte et des gaufrettes. The children have to eat pie and cookies.
Des chèvres avaient à brouter de la sauge et des muguets. Some goats were supposed to graze on sage and lilies
Ces Chinois auront à manipuler de la langoustine et des baguettes. These Chinese will have to handle shrimp and chopsticks.
Certains enfants eurent à manger de la tarte et des gaufrettes. Certain children had to eat pie and cookies.
Les chèvres ont à brouter de la sauge et des muguets. The goats have to graze on sage and lilies.
Des Chinois avaient à manipuler de la langoustine et des baguettes. Some Chinese were supposed to handle shrimp and chopsticks.
Ces enfants auront à manger de la tarte et des gaufrettes. These children will have to eat pie and cookies.
Certains chèvres eurent à brouter de la sauge et des muguets. Certain goats had to graze on sage and lilies.
Les Chinois ont à manipuler de la langoustine et des baguettes. The Chinese have to handle shrimp and chopsticks.
Des enfants avaient à manger de la tarte et des gaufrettes. Some children were supposed to eat pie and cookies.
Ces chèvres auront à brouter de la sauge et des muguets. These goats will have to graze on sage and lilies.
Certains Chinois eurent à manipuler de la langoustine et des baguettes. Certain Chinese had to handle shrimp and chopsticks.
Matrix analyis can help discover the “hidden parameters” of an author's style, and we could consider it as an interesting example of Anoulipism, or the discovery of potentialities in existing texts. The Oulipo believed, however, that Synthoulipism, or the invention of potentialities for future texts, was its “essential vocation”  [Motte 1986, 27]. The combinatorics of non-linear, two-dimensional poems invite the development of computer applications for generating and analyzing a new kind of text. Whether anyone will go to the trouble to write and read matrix poems is a question the Oulipo has not pursued, in part perhaps because it would involve realizing concrete techiques and practices that would no longer be potential.
1
Mathews and Queneau offer two algorithms for creating meaning with language that demonstrate the Oulipo's efforts to imagine potentialities for literature, “if need be through recourse to machines that process information”  [Motte 1986, 27]. We can operationalize these algorithms with computers for literary analysis “if need be”, but the interest of the algorithms lies not in what they help us see in a given text but in the way they invite us to play rigorously for play's sake. Recent efforts to reconceptualize text analysis with computers have tried to imagine how computers can be used as tools for discovering new ways to make sense of texts. The Oulipo proposes something more radical: to borrow a turn of phrase from Jerome McGann, the invention of algorithms can create potentialities for imagining what we do not know about textuality in general. Given a rigorous constraint on the use of language, what does the constraint itself do? Does it offer new possibilities for meaning? If so, how? Oulipian constraints are better understood as toys with no intended purpose rather than as tools we use with some objective in mind. The procedures for making sense of texts are meaningful in and of themselves. They are not only instruments for discovering meaning but also reflections on making meaning. The distinction I have made between writing and reading follows what the Oulipo has and has not articulated in the theory of its practice. In the end, the need for a distinction becomes unnecessary when one observes that all encounters with textuality invite the application of rules that lead the writer and the reader to see unanticipated potentialities in language. Humanities computing should make room for playing with tools without concern for specific output and outcomes. In doing so, it will open itself to new theoretical possibilities of textuality, creating opportunities for what we could call “pure” research that may (or may not) draw interest from the broader humanities community.

Notes

[1] Jerome McGann observes that “In this view of the matter, texts and documents are not primarily understood as containers or even vehicles of meaning. Rather, they are sets of instantiated rules and algorithms for generating and controlling themselves and for constructing further sets of transmissional possibilities” [McGann 2001a, 2].
[2] Readers can use Mathews's Algorithm with their own texts; see http://bumppo.hartwick.edu/Oulipo/Mathews.php.
[3] Readers can perform Queneau's matrix analysis using their own texts; see http://bumppo.hartwick.edu/Oulipo/Matrix.html.
[4] Khmelev and Tweedie selected randomly one text from each of the forty-five authors in their corpus of 387 texts from the Project Gutenberg (http://www.gutenberg.org/). Thirty-three texts were attributed to the correct author, or 73.3 percent, with an error rate of 0.687 percent. Like the sample used by Khmelev and Tweedie, my corpus is composed of texts by authors with at least two texts in the corpus. This allowed me to test Queneau matrices and Markov chains as the basis of an algorithm for identifying authorship.

Works Cited

Bens 1980  Bens, Jacques. Oulipo 1960-1963. Paris: C. Bourgois, 1980. Republished as Genèse de l'Oulipo 1960-1963. Bordeaux: Le Castor Astral, 2005.
Bergens 1999  Bergens, Andrée. Raymond Queneau. 1975. Paris: L'Herne, 1999.
Braffort 1984  Braffort, Paul. “La littérature assistée par ordinateur”, Action Poétique 95 (1984): 12-20.
Braffort 2006  Braffort, Paul. ALAMO: Atelier de Littérature Assistée par la Mathématique et les Ordinateurs. Last accessed 17 September 2006. http://alamo.mshparisnord.net/presentation/index.html.
Bénabou 1980  Bénabou, Marcel. “Un aphorisme peut en cacher un autre”. 1980. La Bibliothèque oulipienne, vol. 1, Paris: Editions Ramsay, 1987, 251-269.
Khmelev and Tweedie 2001  Khmelev, Dmitri V., and Fiona J. Tweedie. “Using Markov Chains for Identification of Writers.” Literary and Linguistic Computing 16.3 (2001): 299-307.
McGann 2001a  McGann, Jerome. Radiant Textuality: Literature After the World Wide Web. New York: Palgrave Macmillan, 2001.
Motte 1986  Motte, Warren F., Jr. “Clinamen Redux”, Comparative Literature Studies.
Olsen 1993  Olsen, Mark. “Signs, Symbols and Discourses: A New Direction for Computer-Aided Literature Studies”, Computers and the Humanities, 27 (1993): 309-314.
Oulipo 1981  Oulipo. 1981. Atlas de littérature potentielle. Paris: Gallimard, 1981.
Oulipo 1998  Oulipo. Oulipo: A Primer of Potential Literature. 1986. Ed. and trans. Warren F. Motte, Jr. Normal, IL: Dalkey Archive Press, 1998.
Queneau 1961  Queneau, Raymond. Cent mille milliards de poèmes. Paris: Gallimard, 1961.
Queneau 1964  Queneau, Raymond. “L'Analyse matricielle du langage”, Etudes de linguistique appliquée (1964): 37-50.
Queneau 1965  Queneau, Raymond. Bâtons, chiffres et lettres. Paris: Gallimard, 1965.
Ramsay 2003  Ramsay, Stephen. “Toward an Algorithmic Criticism”, Literary and Linguistic Computing 18.2 (2003): 167-174.
Reggiani 1999  Reggiani, Christelle. Rhétoriques de la contrainte: Georges Perec — L'Oulipo . Paris: Editions Interuniversitaires, 1999.
Rockwell 2003  Rockwell, Geoffrey. “What is Text Analysis, Really?”, Literary and Linguistic Computing 18.2 (2003): 209-219.
Schmid 2006  Schmid, Helmut. TreeTagger: a language independent part-of-speech tagger. Institute for Natural Language Processing, University of Stuttgart. http://www.ims.uni-stuttgart.de/projekte/corplex/TreeTagger/DecisionTreeTagger.html.
Sinclair 2003  Sinclair, Stéfan. “Computer-Assisted Reading: Reconceiving Text Analysis”, Literary and Linguistic Computing 18.2 (2003): 175-184.
Starynkevitch 1990  Starynkevitch, Dmitri. “The SEA CAB 500 Computer”, Annals of the History of Computing 12.1 (1990): 23-29.
2007 1.1  |  XML |  PDF |  Print
Creative Commons License
This work is licensed under a Creative Commons Attribution-NoDerivatives 4.0 International License.