Works Cited
Alstott et al. 2014 Alstott, J., Bullmore, E., Plenz, D.
power-law: a Python package for analysis of heavy-tailed distributions. PloS One 9, e85777 (2014).
Amaral et al. 2000 Amaral, L.A.N., Scala, A., Barthélémy,
M., Stanley, H.E. Classes of small-world networks. Proc. Natl. Acad.
Sci. 97 ( 2000): 11149–11152.
Araújo et al. 2017 Araújo, C.V.S., Neto, R.M., Nakamura,
F.G., Nakamura, E.F. Using Complex Networks to Assess Collaboration in Rap Music: A Study
Case of DJ Khaled, in: Proceedings of the 23rd Brazillian Symposium on Multimedia and the
Web - WebMedia '17. Presented at the 23rd Brazillian Symposium on Multimedia and the Web,
ACM Press, Gramado, RS, Brazil (2017 ): 425-428.
Barabási et al. 2003 Barabási, A.-L., Bonabeau, E.
Scale-free networks. Sci. Am. 288 (2003): 60–69.
Barrat et al. 2004 Barrat, A., Barthelemy, M.,
Pastor-Satorras, R., Vespignani, A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. 101 (2004): 3747-3752.
Bastian et al. 2009 Bastian, M., Heymann, S., Jacomy, M.
Gephi: An Open Source Software for Exploring and Manipulating Networks, in: Proceedings of the International AAAI Conference on Weblogs and Social
Media (2009)
Bogdanov and Serra 2017 Bogdanov, D., Serra, X.
Quantifying music tends and facts using editorial metadata from the Discogs database, in:
Hu X, Cunningham SJ, Turnbull D, Duan Z. ISMIR 2017 Proceedings of
the 18th International Society for Music Information Retrieval Conference
(2017): p. 89-95.
Brandes et al. 2011 Brandes, U., Eiglsperger, M., Herman,
I., Himsolt, M., Marshall, M.S., 2001. GraphML progress report structural layer proposal,
in: International Symposium on Graph Drawing. Springer, pp.
501–512.
Burgoyne et al. 2016 Burgoyne, J.A., Fujinaga, I.,
Downie, S. Music Information Retrieval, in: Schreibman, S., Siemens, R., Unsworth, J.
(Eds.), A New Companion to Digital Humanities. Wiley
Blackwell, West Sussex (2016).
Filipova et al. 2012 Filippova, D., Fitzgerald, M.,
Kingsford, C., Benadon, F. Dynamic Exploration of Recording Sessions between Jazz
Musicians over Time, in: 2012 International Conference on Privacy, Security, Risk and
Trust and 2012 International Conference on Social Computing,
IEEE, Amsterdam, Netherlands (2012): 368–376.
Giaquinto et al. 2007 Giaquinto, G., Bledsoe, C.,
McGuirk, B. Influence and similarity between contemporary jazz artists, plus six degrees
of kind of blue. PhD Thesis (2007).
Gioia 1998 Gioia, T. The History of
Jazz. Oxford University Press, USA (1998).
Girvan and Newman 2002 Girvan, M., Newman, M. Community
structure in social and biological networks. Proc. Natl. Acad.
Sci. 99 (2002): 7821–7826.
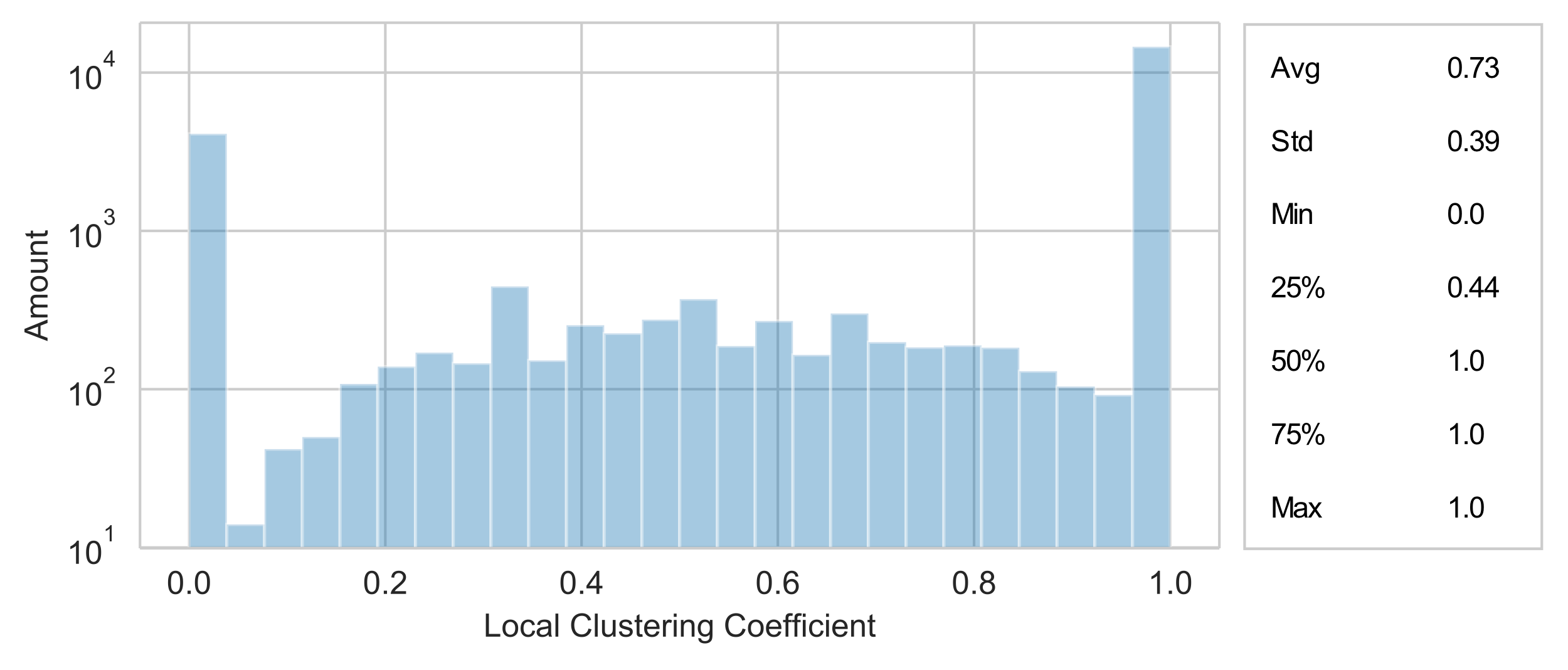
Gleiser and Danon 2003 Gleiser, P.M., Danon, L. Community
structure in jazz. Adv. Complex Syst. 6 (2003):
565–573.
Hagberg et al. 2008 Hagberg, A., Swart, P., S Chult, D.
Exploring network structure, dynamics, and function using NetworkX. Los Alamos National
Lab. (LANL), Los Alamos, NM, United States (2008).
Hammou 2014 Hammou, K. Between social worlds and local
scenes: Patterns of collaboration in francophone rap music, in: Social Networks and Music Worlds. Routledge (2014): 128–145.
Hannibal 2015 Hannibal, B. The Network Influences of
Innovation and Lifetime Career Success in Jazz Musicians between 1945 and 1958. PhD Thesis
(2015).
Hinton et al. 1988 Hinton, M., Berger, D.G., Morgenstern,
D., 1988. Bass line: the stories and photographs of Milt
Hinton. Temple University Press.
Jockers 2013 Jockers, M. L. (2013). Macroanalysis: Digital methods and literary history. University of Illinois
Press.
Macdonald and Wilson 2006 Macdonald, R.A.R., Wilson,
G.B. Constructions of jazz: How Jazz musicians present their collaborative musical
practice. Music. Sci. 10 (2006): 59–83.
Makkonen 2017 Makkonen, T. North from here: the
collaboration networks of Finnish metal music genre superstars. Creat. Ind. J. 10 (2017): 104–118.
Mertl et al. 2008 Mertl, V., O'Mahony, T.K., Tyson, K.,
Herrenkohl, L.R., Honwad, S., Hoadley, C. Analyzing collaborative contexts: Professional
musicians, corporate engineers, and communities in the Himalayas, in: Proceedings of the 8th International Conference on International Conference for the
Learning Sciences-Volume 3. International Society of the Learning Sciences
(2008): 282–289.
Newman 2001 Newman, M. The structure of scientific
collaboration networks. Proc. Natl. Acad. Sci. 98 (2001):
404–409.
Newman 2003 Newman, M. The structure and function of
complex networks. SIAM Rev. 45 (2003): 167–256.
Newman 2010 Newman, M. Networks: An
Introduction, 1st ed. Oxford University Press (2010).
Park et al. 2007 Park, J., Celma, O., Koppenberger, M.,
Cano, P., Buldú, J.M. The social network of contemporary popular musicians. Int. J. Bifurc. Chaos 17 (2007): 2281–2288.
Park et al. 2015 Park, D., Bae, A., Schich, M., Park, J.
Topology and evolution of the network of western classical music composers. EPJ Data Sci. 4, 2 (2015).
Patuelli et al. 2011 Pattuelli, C., Weller, C., Szablya,
G. Linked Jazz: An Exploratory Prototype, in: International
Conference on Dublin Core and Metadata Applications. Dublin, Ireland (2011):
158–164.
Phillips and Kim 2009 Phillips, D.J., Kim, Y.-K. Why
pseudonyms? Deception as identity preservation among jazz record companies, 1920–1929.
Organ. Sci. 20 (2009): 481–499.
Schilling and Phelps 2007 Schilling, M.A., Phelps, C.C.
Interfirm collaboration networks: The impact of large-scale network structure on firm
innovation. Manag. Sci. 53 (2007): 1113–1126.
Seddon 2005 Seddon, F.A. Modes of communication during
jazz improvisation. Br. J. Music Educ. 22 (2005):
47–61.
Seddon and Biasutti 2009 Seddon, F., Biasutti, M. A
comparison of modes of communication between members of a string quartet and a jazz
sextet. Psychol. Music 37 (2009): 395–415.
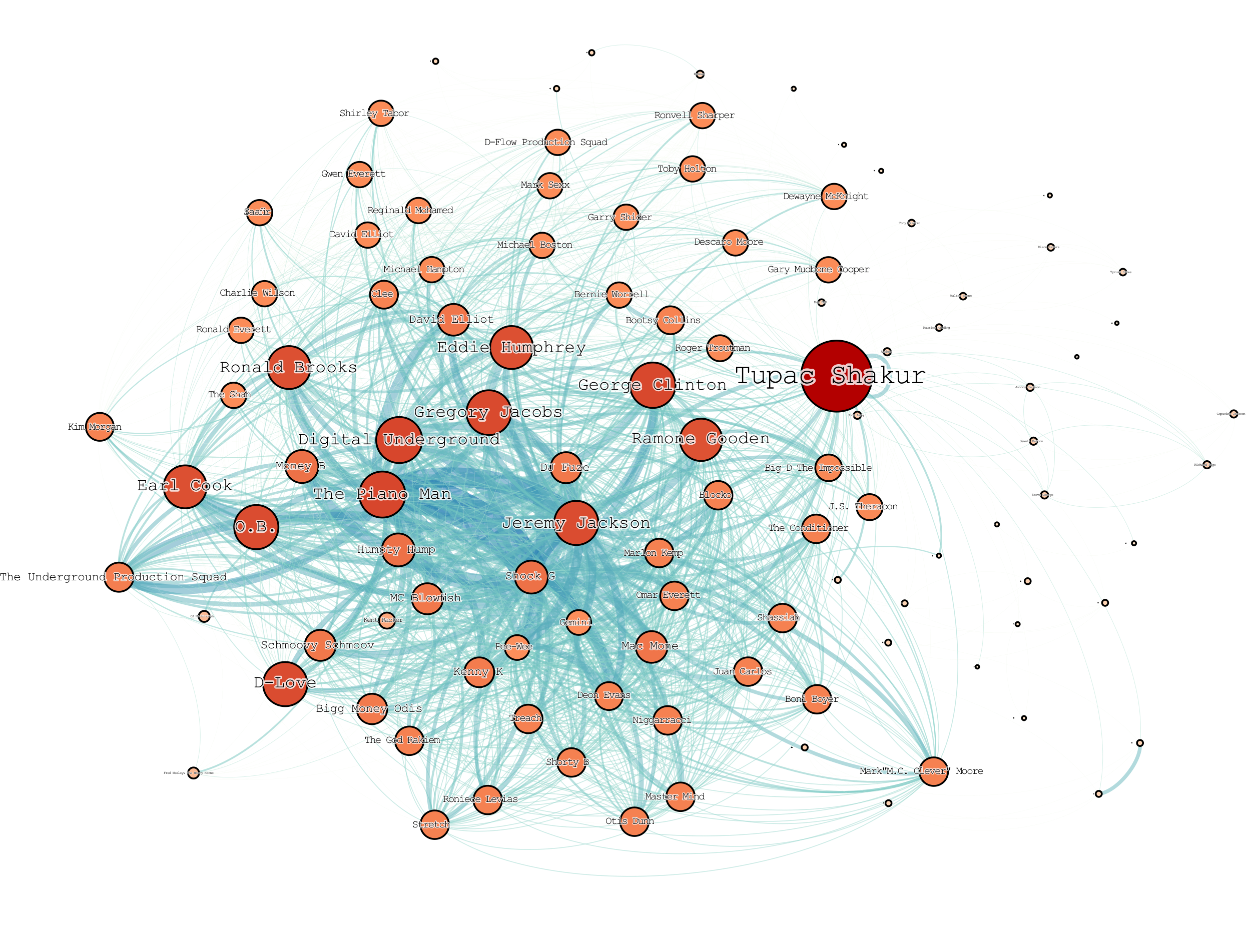
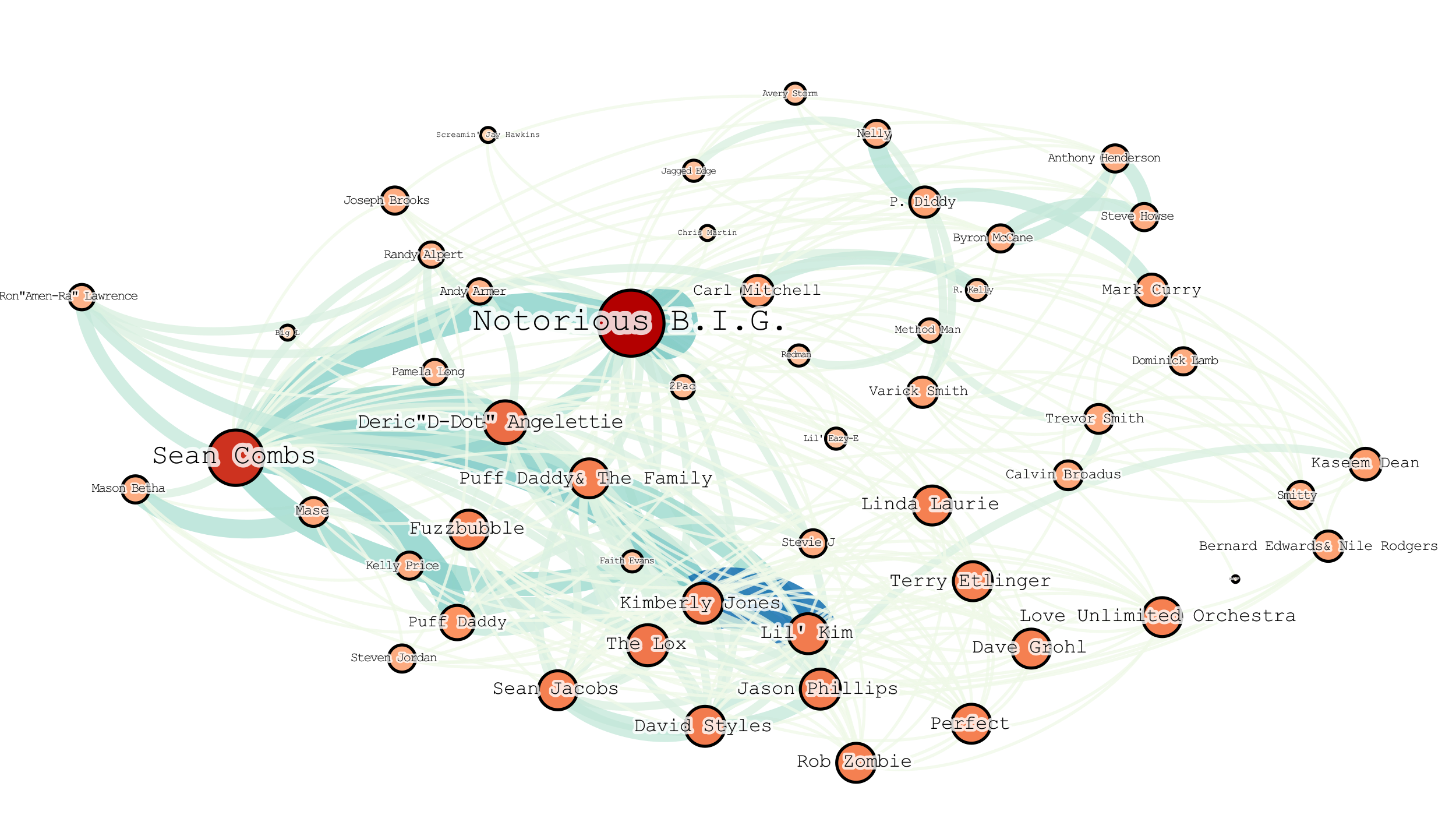
Smith 2006 Smith, R.D. The network of collaboration among
rappers and its community structure. J. Stat. Mech. Theory Exp.,
P02006 (2006).
Smith 2016 Smith, S. Hip-Hop
Turntablism, Creativity and Collaboration, Routledge (2016).
Teitelbaum et al. 2008 Teitelbaum, T., Balenzuela, P.,
Cano, P., Buldú, J.M. Community structures and role detection in music networks. Chaos Interdiscip. J. Nonlinear Sci. 18, 043105 (2008).
Watts and Strogatz 1998 Watts, D.J., Strogatz, S.H.
Collective dynamics of 'small-world' networks. Nature 393
(1998): 440.
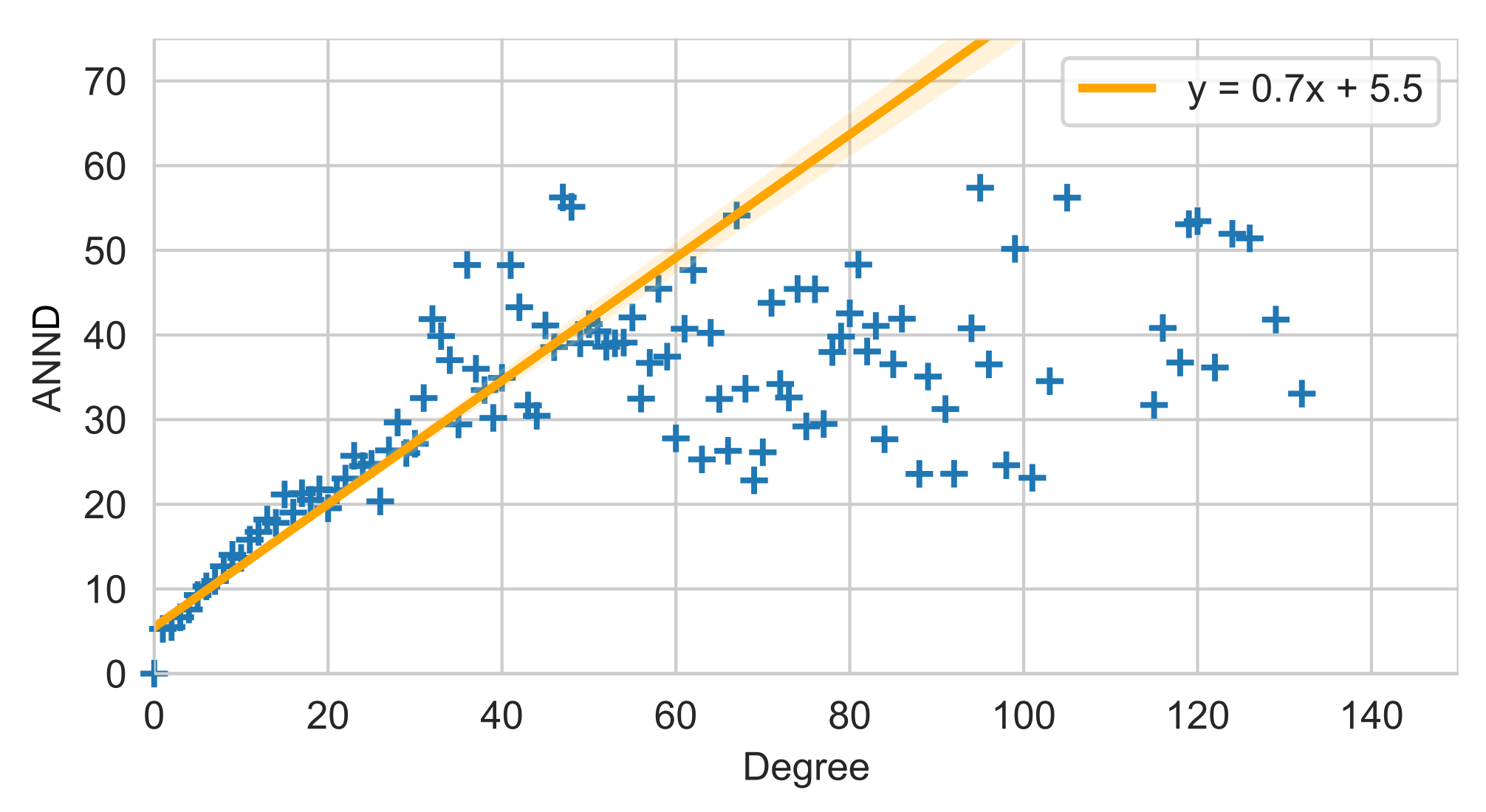
Yao et al. 2017 Yao, D., van der Hoorn, P., Litvak, N.
Average nearest neighbor degrees in scale-free networks. ArXiv Prepr.
ArXiv170405707 (2017).
Zhang et al. 2006 Zhang, P.-P., Chen, K., He, Y., Zhou, T.,
Su, B.-B., Jin, Y., Chang, H., Zhou, Y.-P., Sun, L.-C., Wang, B.-H., others. Model and
empirical study on some collaboration networks. Phys. Stat.
Mech. Its Appl. 360 (2006): 599–616.
de Lima e Silva et al. 2004 de Lima e Silva, D., Medeiros
Soares, M., Henriques, M.V.C., Schivani Alves, M.T., de Aguiar, S.G., de Carvalho, T.P.,
Corso, G., Lucena, L.S. The complex network of the Brazilian Popular Music. Phys. Stat. Mech. Its Appl. 332 (2004): 559–565.