DHQ: Digital Humanities Quarterly
2023
Volume 17 Number 3
Volume 17 Number 3
Are Ontologies Trees or Lattices?
Abstract
Ontologies, it is sometimes said, take the form of a hierarchy or tree: each class is subdivided into distinct subclasses with no cross classifications. But if the purpose of an ontology is to make possible useful inferences and to guide software users and developers, it is better to allow a more flexible structure. Using text annotation as an example (with concrete reference to the CATMA annotation tool), we argue that it will be more useful to structure ontologies as lattices, not trees.
If taken literally, our title question would have a trivial and negative answer. Ontologies are not simply trees, nor are they simply lattices, just as territories are not (simply) maps. Graphs (and trees and lattices, as subspecies of graphs) are defined mathematically as consisting of a set of vertices (or nodes) and a set or bag of edges (or directed arcs) connecting them.
There is more to ontologies than just that. So when we ask “Are ontologies trees?” we mean, “Can ontologies usefully be modeled as trees, and if so, how and under what circumstances?” And similarly for lattices. As there is no rule that only one abstract model can be useful in a given context, the two possibilities mentioned are neither exhaustive nor mutually exclusive.
The context in which we are aiming to give an answer to our question is that of ontologies applied to annotations and annotation schemes. Our examples are taken from use of the textual annotation tool CATMA [Gius et al. 2022], with particular attention to possible restructuring of existing annotation tag sets, and possible export of annotation data to reasoning systems.[1]
Our aim is to show that in a context like this, ontologies constructed around the superset and subset relations on classes and modelled as lattices are more flexible and useful than ontologies modelled as trees. Our evaluation criteria are concrete and rather simple: does the structure chosen for the ontology make it easier or harder for users or software developers to define and perform certain obvious tasks that will arise in any annotation system like CATMA? We hope that our references to CATMA provide a concrete application of our argument which may make it easier to follow, but we believe that our findings are relevant for ontologies in general.
We begin by defining some terms and articulating some assumptions. We then describe some salient features of CATMA and their ontological implications. We argue that annotations are best understood as attributing properties to text passages and best formalized using predicates which hold of text passages. Against that background, we proceed to discuss advantages and disadvantages of modelling an ontology for annotation as a tree, and the comparative advantages of modeling it instead as a lattice. We believe that the natural model for an ontology of text annotations is not a tree, but a lattice.
Definitions and assumptions
Ontology, according to Webster's New international dictionary of the English language, is “The science of being or reality; the branch of knowledge that investigates the nature, essential properties, and relations of being, as such” [Webster's 1923].
For purposes of the present discussion, we will apply the name “ontology” to any attempt to say what kinds of things exist in any domain, or universe of discourse, and to give some account of their properties and relations to each other. Such attempts are often more or less systematic, but that is not essential to our usage.
One useful tool for deciding what exists is the so-called criterion of ontological commitment. According to Quine, “a theory is committed to those and only those entities to which the bound variables of the theory must be capable of referring in order that the affirmations made in the theory be true” [Quine 1948, 13–14].[2] In philosophy, Quine's criterion has been very influential and is still a matter of considerable discussion. Since it is readily applied in formal and easily formalizable systems, it has also had a wide uptake in computing contexts, where it makes possible the comparison of ontological commitments in various approaches to modeling a problem.[3]
A classification scheme is for our purposes here any set of classes intended for application in some universe of discourse, together with rules for assigning things to classes; like ontologies classification schemes are often but not necessarily systematic. Any ontology includes a set of classes containing (and implicitly characterizing) things that exist, and thus a classification scheme. Conversely, any classification scheme identifies different kinds of things that can exist and thus entails an ontology. So although there may be (and usually is) more to an ontology than just a classification scheme, we regard the theory of classification as relevant to ontology, and vice versa.
Most classification schemes intended for practical use group items together into classes on the basis of certain characteristic properties which are necessary and sufficient for identifying the item as a member of the class. For any given class, some set of items in the universe of discourse will fall into that class, and other items will fall outside that class. The set of items falling under the class is its extension; the set of characteristic properties of a class is its intension.
The properties used in different classification schemes vary widely; for our examples, we use properties like being human, being male, being an adult or an adolescent or a child, and so forth. Properties may be combined: individuals who have the properties of being human, being female, and being adult may be said to have the property of being women (adult female humans).
Intension and extension typically are in inverse proportion to each other: the more properties are specified in the intension of a class, the smaller its extension will become. For example, the set of all humans has a larger extension and a smaller intension than the set of all women (adult female humans). Note that adding properties to the intension of a class is not guaranteed to decrease its extension (the class of adult humans who are authors of this paper, for example, has a smaller intension than the class of adult male humans who are authors of this paper, but the two classes have the same extension), but it never increases it.
We assume that any property can be represented formally by a predicate. We understand predicates to be functions which map objects or tuples of objects in the universe of discourse (the arguments of the function) to the truth values true or false. For example, the property of being an adult female human may be represented formally by the predicate is_a_woman, which takes one argument and is true for just those individuals in the universe of discourse who are women. Both the term predicate and the analysis of propositions in this way echo the traditional grammatical analysis of sentences as consisting of a subject and a predicate. Of particular importance for any class of objects is the characteristic predicate of the class (also commonly called its characteristic function), which returns the value true for all members of the class and false for all other individuals.
In the sentence “Gottlob Frege was born in 1848,” for example, the predicate is “was born in 1848” and the subject (or argument of the predicate) is “Gottlob Frege”. In formulae we might write this as was_born_1848(Frege). Predicates may have more than one argument: the more general predicate name_yearofbirth(x, y) (in words: “x was born in the year y”) takes two arguments, one for an individual and one for a year. We can say (truthfully) that Frege was born in 1848 by asserting either was_born_1848(Frege) or name_yearofbirth(Frege, 1848).
The number of arguments taken by a predicate is called its arity; predicates of arity one and two are often called unary and binary predicates, respectively, and predicates of unspecified arity may be referred to as n-ary predicates.
It should be noted that a predicate of lower arity may be equivalent to a predicate of higher arity with a fixed (or: constant) value for a given argument: we may define was_born_1848(x) (in words: “x was born in 1848”) as true for the same set of x as name_yearofbirth(x, 1848). And similarly, the unusual but semantically well formed predicate Frege_was_born_in(x) would be true for precisely those x for which name_yearofbirth(Frege, x) is true. Here “1848” and “Frege” are constant values, not variables.
Any predicate P(x) identifies a set, which is operationally the set of all x such that P(x) is true: in a formula, {x | P(x)}. And conversely, for any set S there will be at least one possible predicate P whose extension is S. (As a last resort, we can always define P as the property “is a member of S”.)[4]
It will be observed that any set of predicates may serve as the basis of a classification system and thus of an ontology, and conversely that the characteristic properties of the classes of any classification scheme can be represented formally by some set of predicates.
In attempting to answer the question posed in our title, we make some assumptions that may be worth trying to make explicit here. We assume (among other things):
- Regarding the organization of tags in an annotation scheme as an ontology has no particular merit in itself; the point of thinking of an annotation scheme as an ontology is to help solve problems.
- Those served (or not) by an ontological view of an annotation scheme include the annotators, the users who search annotated documents and visualize the results, and the developers of the annotation software. (In our concrete example: both CATMA users and CATMA developers.)
- An ontological view of the annotation scheme can help annotators and searchers by helping them create an intuitive understanding of the logical or semantic structure of the annotation scheme (what tags are related to what other tags, and how tags can be similar or different in meaning).
- By providing names for properties and combinations of properties, an annotation scheme can make it easier (or harder) to think and talk about particular phenomena. In this context, simple one-word names tend as a rule to be easier to work with (think with, talk with) than combinations of names. (For example: it is usually easier to say “woman” than to say “living adult female of the species homo sapiens”.)
- Ontology can help software developers by making it easy to support user interfaces that exploit the semantic relations of tags. Semantic information about tags can be helpful in various interfaces, for example:
- annotation, e.g. in the tasks of navigating through the tag set and selecting the appropriate tag for a given passage;
- management of the annotation scheme, e.g. in the task of restructuring an annotation scheme on the basis of experience, to make it more expressive or to make it easier to apply commonly needed tags;
- search, e.g. in the task of specifying which classes of annotation are relevant to the search.
- Because ontologies typically describe explicitly how different classes of things are similar and different, they are also commonly used to guide logical inference. Ontologies can be evaluated on the kinds of inferences they make easy.
- Ontologies and structures for ontologies can be evaluated both on their expressive power (what one can and cannot say, in the terms provided by a given ontology or class of ontologies) and on their convenience (how easy it is to say it).
Annotation in CATMA
“CATMA” stands for “Computer Assisted Text Markup and Annotation”. The CATMA web application provides tools for text annotation and analysis. Its primary target audience is humanities scholars, among (and beyond) which it has gained a wide audience.[5] Among the reasons for its wide uptake are probably the combination of a very easy-to-learn and easy-to-use annotation interface, a wide range of tools for visualization and analysis, and its support for exploratory and cooperative work. See [Gius et al. 2022].
In CATMA's terms, an annotation scheme is a tag set. A tag set consists of one or more tags, each with zero or more subtags, which may or may not in turn have their own subtags, and so on. A tag with subtags is called their supertag. Tags may be furnished with named properties[6] which may in turn carry values.
CATMA provides a search interface in which the user can search the document for the occurrence of words or strings of characters, or of specific tags or combinations of tags. Visualization tools make it possible to compare the pattern of occurrences of different tags, or of the same tags in different documents. Data can be exported for further processing using other tools.
Annotation starts by uploading a document and selecting a tag set. The document is displayed in a pane in the left half of the window, while the right pane displays the tag set. Annotations are added to the text by highlighting a text passage, choosing the tag with which to annotate it, and selecting values for the tag's named properties (if any).
Users may revise the tag set by adding, deleting or changing tags as they go along. Unlike some other annotation tools, CATMA allows the user to start with an empty tag set.
Text passages carrying an annotation may be discontinuous, and they may overlap. There is no requirement that a text passage annotated with a supertag should contain passages annotated with that supertag's subtags. Similarly, there is no requirement that a text passage annotated with a subtag should be contained in a passage annotated with that subtag's supertag. (For any text passage annotated with a subtag, however, CATMA will assume that its supertag applies.) In other words, CATMA does not enforce a tree-like hierarchical ordering of the annotations of a document.
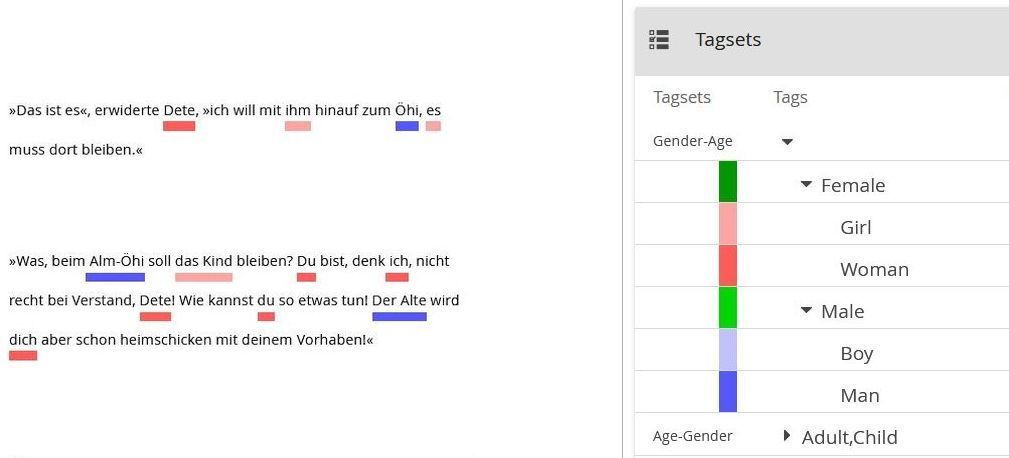
In our context, however, it is not the structuring of the document, but the structuring of the annotation scheme, i.e. of the CATMA tag set, that is of primary interest. And in CATMA the structure of the annotation scheme is indeed hierarchical.[7] As such, it illustrates a dilemma discussed further below. We may choose to organize a tag set for demographic annotation of human characters first by gender and then by age. In CATMA, it might look like this:[8]
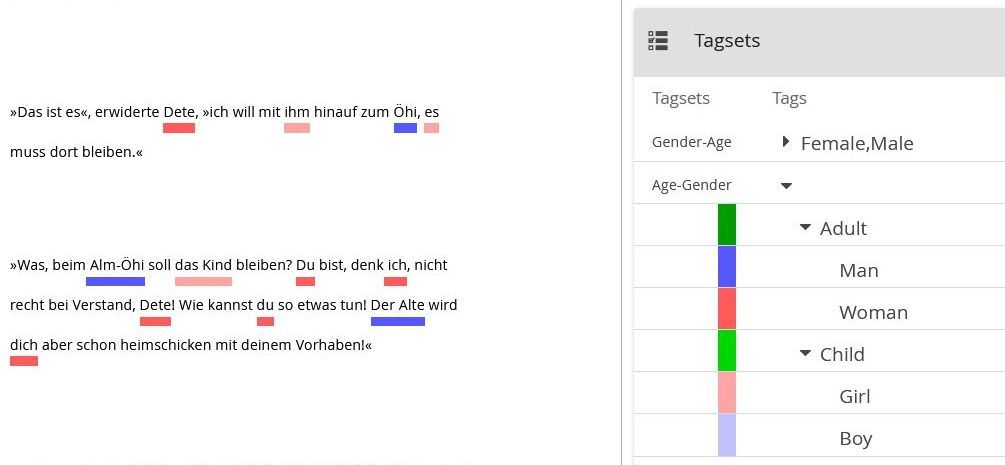
Alternatively, we might organize the annotation scheme first by age and then by gender, like this:
Both tag sets provide for the same subtags (Woman, Girl, Man, Boy). The first tag set groups them into the supertags Female and Male, the second tag set groups them into the supertags Adult and Child. Using the first tag set it is straightforward to locate all passages annotated as relating to Female characters or to Male characters, but there is no easy way to locate all passages relating to Adult[s] or to Child[ren]. With the second tag set it is the other way around.[9]
An ontological view of CATMA annotations
It may be helpful to relate the features of CATMA described above to our discussion of ontologies, considering several questions in turn.
Annotation classes and properties
When a CATMA user defines annotation classes (tags) and arranges them in a class/subclass (tag/subtag) hierarchy, the user is specifying what kinds of annotations shall exist (when it comes to annotation classes, what there is is what the user says there is). Any CATMA tag set is thus a classification scheme for annotations (since each annotation is created as an instance of some specific annotation class (tag)), and implies an ontology.
As noted above, we assume that for any class in a classification scheme there exists a characteristic property which holds for all and only the things belonging to the class, and that every such characteristic property can be represented formally by a characteristic predicate. In the case of annotations, the salient property is the one attributed by annotations of that class to passages in the text.[10]
It should be noted that in CATMA as in other annotation systems, the user is not required to identify the characteristic property of an annotation class or to formulate its characteristic predicate explicitly; both the characteristic property and the characteristic predicate are typically left implicit. For purposes of our argument, we are observing that they exist, not assuming that they have been explicitly defined.
The intension of any tag will as always be a set of properties to be attributed to text passages. It follows from the logic of the class hierarchy that the intension of a subtag will include the intension of its supertag. And the extension of any subtag will, by construction, be a subset of the extension of its supertag.
In the following discussion we will consider annotation classes as classifying both annotations and their target text passages. The extension of any annotation class thus contains both a set of annotations and the set of text passages annotated, and the intension of the class may involve both properties of text passages and properties of other things in the universe of discourse. When it is necessary to do so, we may single out the set of annotations or the set of text passages in the extension, or the different kinds of properties involved in the intension.
The ontological commitments of annotation
Because it can handle conflicting views of the world with equanimity, Quine's method of approaching ontology by identifying ontological commitments in already-held beliefs has, we think, potential interest and utility for annotators and for CATMA's system designers. For CATMA, the ontological commitments of concern are the ones made by annotators in declaring annotation classes and in annotating documents. CATMA seeks to minimize its own ontological commitments, in order to avoid imposing them on annotators.
It is of course true that annotations made by different annotators (or even by the same annotator) may conflict in various ways. It is also true that an annotator may be right or wrong in annotating (or not annotating) a text passage with a certain tag. We do not believe that this in itself is likely to lead to logical inconsistencies in an annotation ontology, since the only facts whose consistency is at issue are facts about what has actually been annotated how in some concrete sets of documents. For our purposes, we can regard those as brute facts.
The annotation scheme classifies annotations, and thus entails an ontological commitment to the existence of annotations. Each annotation attributes some property to some passage of the text. The ontology underlying annotation in CATMA thus also necessarily entails the existence of text passages.[11]
The reader may at this point ask whether the idea that an annotation attributes a property to a text passage also entails a commitment to the existence of properties as a nameable kind of thing. The answer, we believe, is that it depends on the annotation software. CATMA and other annotation systems provide interfaces which allow the user to ask, in effect, what annotations apply to a given text passage, or conversely what text passages are marked with a given tag (which is to say, what text passages fall into a given class).
We can formalize the membership of an annotation a in a class C with the predicate C(a) and the relation of a to a text passage x as annotates(a, x). Sentences of these forms will be the “affirmations made in the theory” for purposes of applying Quine's criterion for existence. Given such a formalization, the user interface actions mentioned above can be interpreted as finding particular sets: the set of all annotations for a given passage x is the set {a | annotates(a, x)} (read “the set of all annotations a such that a annotates x”), and the set of all passages of a given class C of annotations is the set {x | (∃a)(annotates(a, x) and C(x))} (read “the set of all passages x such that there exists some annotation a which annotates x and for which C(x) holds”).
When named properties are queried, the queries may become slightly more complex, but follow the same pattern. For example, if the tag set had a single Person tag, with named properties for age and sex, and subtags like Child, then one might wish to search for occurrences of Child with age greater than 16, to check the consistency of the annotations. Let us use Person(a) and Child(a) to identify all annotations using those two tags, and Person_age(a, n) to denote the relation holding between a Person or Child annotation a and the value n of its named property age. Then a search for all text passages marked as concerning a child with age greater than 16 is a search for the set {x | (∃a)(annotates(a, x) and Child(x) and (∃n)(Person_age(x, n) and n > 16))}.
The user interfaces described thus do not commit the annotation system to the existence of properties; in the formalization just sketched, there are no references to, or variables denoting, properties. Informal reference to “properties” in English prose can be taken as just a manner of speaking about particular predicates. It might be that a different annotation system could offer operations which would entail an ontological commitment to the existence of properties, but thus far we have not managed to think of any plausible operation which would require such a commitment.
Two practical uses of ontology for text annotation systems
The hierarchical structure of the tag set has two important practical uses. First, it allows an annotation interface to present tags for selection using menus and submenus whose structure reflects the user-defined hierarchy of the tag set. (From a strictly philosophical point of view this may appear a minor point; from the user interface point of view, it is not minor.)
Second, the supertag/subtag relation and the implicit relation of their intensions licenses simple but important inferences about the properties of annotations and text passages: every passage marked with the subtag may safely be inferred to possess the properties in the intension of the supertag, and thus to be legitimately treated as an instance of the supertag. In practice this means that it is convenient to be able to ask an annotation system to identify all instances of a tag and have the software return all annotations marked with either that tag or with any of its subtags, subsubtags, and so on to all levels of subtag. It is the fact that subtags inherit the intension and contribute to the extension of their supertags which justifies this inference and makes it meaningful to allow the user to search for all instances of female annotations and be shown instances of the subtags girl, woman, etc., or to search for all instances of adult annotations and be shown instances of man, woman, etc.[12] A clear understanding of the inferences licensed by the tag set's structure may make it easier to export annotations for processing using reasoning systems.
There may be other uses for the ontology implicit in a CATMA tag set, but for our further discussion we restrict ourselves to these two: guidance for the user interface and annotation-management tools, and logical inference about the properties of annotations and text passages.
Logical form and inferences
We said above that the universe of discourse relevant to a CATMA annotation scheme (tag set) includes both annotations and text passages, and that each annotation class (tag) is associated with some property that may hold of text passages. This is true but not the full story. Some predicates take multiple arguments, and we need to extend our account to accommodate such predicates.
Simple tags and unary predicates
Every annotation annotates some text passage; as noted above, from our point of view this amounts to saying that every annotation asserts the presence of some property in the text passage annotated. (For technical reasons we are excluding the possibility of meta-annotation.) It follows that every predicate representing the property associated with an annotation class must have at least one argument position for a text passage. For the moment, we limit our discussion to tags whose characteristic predicate has only that one argument (and is thus a unary predicate), which we will refer to as simple tags.
Simple tags have a straightforward representation in symbolic form: for every simple tag t there is some characteristic predicate Pt, which takes a single argument of type text-passage.[13] For example, suppose a project interested in gender and age roles marks passages in which characters of different ages and genders are mentioned, with the aim of comparing the vocabulary used for males and females, or for children and adults. The project may have tags named woman, girl, man, boy, each marking a passage in which a woman, girl, boy, or man is mentioned. The characteristic predicates of these tags might be woman(x), girl(x), man(x), boy(x), where x in each case is a variable denoting a text passage. Generic tags female, male, child, and adult might also be provided, in case a reference is specific in one way but not in the other.
If the generic tags are used as supertags and the more specific tags as subtags, the logical relation of the subtags to the supertags can be expressed formally in a very simple way: for any supertag A and subtag B, with characteristic predicates of the same name, the meaning of the subtag / supertag relation is “any annotation in class B is also in class A,” or equivalently “any text passage which exhibits property B also exhibits property A.” Formally, this can be expressed by the logical expression
This may be read “For all x, if B(x) applies, then A(x) applies”, or “For any x, if x has property B, then x has property A.”(∀ x)(B(x) ⇒ A(x))
More concretely, if male and female are used as supertags for the age and gender tag set, the inference rules will take forms like this:
Note that the following inference rules also apply, given the meanings indicated for these tags, but will be known to the system automatically only if a subtag can have two different supertags. If a tag set must form a strict hierarchy, these inferences will not be automatic.(∀ x)(girl(x) ⇒ female(x))
(∀ x)(woman(x) ⇒ female(x))
(∀ x)(boy(x) ⇒ male(x))
(∀ x)(man(x) ⇒ male(x))
An annotation system might conceivably allow the user to specify inference rules like these explicitly, but that seems unlikely to make the user interface seem simple and intuitive. For that reason we are particularly interested in ways that allow the applicable inference rules to be constructed automatically from the ontology specified by the user in the course of defining the tag set.(∀ x)(girl(x) ⇒ child(x))
(∀ x)(woman(x) ⇒ adult(x))
(∀ x)(boy(x) ⇒ child(x))
(∀ x)(man(x) ⇒ adult(x))
Tags with named properties and n-ary predicates
Often, the properties we wish to discuss hold not of a single individual but of two or more individuals as a group. In symbolic logic, such properties are conventionally represented using predicates which take more than one argument. A sentence might take the form P(x, y) or P(x, y, z), instead of just P(x). See, for example, the discussion above about ways of representing the proposition that Frege was born in 1848.
As mentioned above, CATMA allows the definer of a tag set to associate a set of named properties with each tag, with suggested values for each. When creating an annotation, the annotator can supply a value for each named property, selecting one of the suggested values or supplying a different one. Thus instead of the tags woman, girl, man, and boy described in the preceding section, our imaginary tag set for age and gender roles might have a single tag character, with the named properties age (with suggested values like infant, child, adolescent, adult) and gender (with suggested values like male, female, and 3d-sex.[14] The characteristic property of character might then be formulated as “[this passage] describes a character with the indicated age and gender”, and its characteristic predicate might be written character(x, y, z), where x is a text passage, y a keyword indicating an age, and z a keyword indicating gender. The logical representations for passages describing women, girls, men, and boys might take forms like these:
character(x, adult, female)
character(x, child, female)
character(x, adult, male)
character(x, child, male)
Supertag/subtag relations and n-ary predicates
The logical relations of the characteristic properties of different tags become a little more complex when the tag-set design patterns described in the preceding sections are used together.
Logically speaking, a single character tag suffices for the purposes described. But using it can be slightly tedious, requiring that the annotator mark a passage, select the tag, and then specify values for one or more named properties. It is perceptibly more convenient just to mark a passage and choose a tag. So for practical purposes, we might want a generic character, with named properties as described above, and also a set of more specific subtags for use in common cases: girl, woman, etc. Such a tag set can be put to good use, with appropriate support from the annotation system. Some of the desiderata are not (as far as we know) now supported by CATMA, so in the following discussion, our descriptions of things that annotation software might do are not descriptions of existing software but of software that could be constructed and which would (we think) be useful to those designing tag sets and restructuring their tag sets in the light of experience with their use on real texts.
But what kinds of support would be helpful, and how can the ontology implicit in the design of the tag set be used to allow that support?
Let us consider the case of a trope tag for marking of rhetorical tropes. An annotator might start work with just the one tag, using a named property (say, type) to identify the specific figure of speech appearing in the text, with a list of suggested values: metaphor, metonymy, synecdoche, and irony, with other values to be supplied during annotation as needed. As annotation proceeds, the annotator decides that it would be convenient to have one-click tags for metaphor, metonymy, synecdoche, and irony. The idea is that tagging a passage as a metaphor should be equivalent to tagging it as a trope with the named property type given the value “metaphor”, and similarly for the other subtags.
This can be formalized in either of two ways. If the subtags are assumed to have unary characteristic predicates, and the supertag a binary characteristic predicate, then the appropriate inference rules would be
(∀ x)(metaphor(x) ⇒ trope(x, metaphor))
(∀ x)(metonymy(x) ⇒ trope(x, metonymy))
(∀ x)(synecdoche(x) ⇒ trope(x, synecdoche))
(∀ x)(irony(x) ⇒ trope(x, irony))
In simple cases like this one, where each subtag has a name identical to a suggested value of a named property on the supertag, we can imagine a user interface that allows a user to define the supertag and then request that a subtag be generated automatically for each suggested value of the named property. The system could also search systematically for uses of the supertag with the suggested values, and re-tag them using the new subtag.
Another approach to this operation would use the same characteristic predicate for the supertag and each subtag, so that instead of the characteristic predicates metaphor(x), metonymy(x), synecdoche(x), and irony(x), the subtags would have the characteristic predicates
- trope(x, metaphor)
- trope(x, metonymy)
- trope(x, synecdoche)
- trope(x, irony)
- (∃y)(trope(x, y))
If the supertag has more than one named property (like the character tag), then the user will need to specify which named properties to use for generating the subtags, and the user may well need to provide the names of the subtags. If the character tag has two named properties with exhaustive lists of possible values:
- age: one of infant, child, adolescent, adult
- gender: one of male, female, 3d-sex
Also useful, but perhaps more challenging both from a logical point of view and for the software developer, would be analogous operations which group an existing set of tags together as subtags of a new supertag. Let us imagine that an annotator has begun work on a novel by tagging the places at which specific characters are described: in the case of Heidi, the annotator might have created tags for most of the speaking characters: Heidi, Dete, the Alpen-Ohi, Peter, and so on. The annotator may then realize that for purposes of analysis it would be helpful to treat all female characters as a class, and similarly for the males, so they may wish to create new supertags for female and male characters. In this case, the characteristic predicates constructed by the software are all likely to be unary predicates. The user might then create the appropriate named properties for the supertags and describe how the named properties and their values apply to the subtags, but otherwise the software can have no basis for constructing any n-ary characteristic predicates.
The operations described so far can all be offered in an annotation system with hierarchical annotation ontologies, at least in a limited way, but we think the system can be more useful if the hierarchical constraint is relaxed, so that existing subtags can be grouped together into multiple overlapping supertags: girl and woman being grouped into female characters, while girl and boy are grouped together into child.
Other patterns are doubtless possible for the automatic creation of subtypes from supertypes, or the grouping of types into a new supertype. We hope, however, that the simple examples we have described illustrate ways in which software can provide convenient facilities for managing and restructuring an annotation tag set in coherent and consistent ways, if the software is built to pay attention to the characteristic predicates implicit in the definitions of tags, and to the logical relations among characteristic predicates implied by the ontology of the tag set.
Are ontologies trees?
In its current version, CATMA requires that tag sets be organized into sets of hierarchically ordered classes. But nothing in the definitions of ontology and classification schemes offered above entails that an ontology or classification scheme must be structured in this way.
There is however a fairly widespread idea that a properly specified ontology ought to define a hierarchy, and many influential ontologies and classification schemes do so. For example, a recent white paper on best practices of ontology development insists that: “All ontologies include one or more central backbone hierarchies in which the relation of subtype (aka is_a) connect the nodes. Each backbone hierarchy has a single root node” [Rudnicki et al. 2016].[16]
If we start with a collection of physical objects and seek to organize them, it is natural or at least common to partition them first into subgroups according to some property and then to partition each subgroup in turn according to further properties, repeating the process until the resulting groups are felt to need or allow no further division. (A set of subclasses partitions a superclass if and only if every member of the superclass is a member of exactly one subclass.)
For example, an anthropological museum might organize artefacts first by the source culture and then by function, or (as in the case of the Pitt-Rivers museum in Oxford) first by function and then by source. Any such procedure of repeated division of a group into subgroups will produce a set of classes nesting in other classes, which can be understood as forming a hierarchy, or (what amounts to the same thing) a (rooted) tree.
For classifications that do not involve physical objects, the primary advantage of unique assignment to classes in a hierarchy appears to be the ability to calculate sums without including anything twice. But while guidance for the physical arrangement of objects and assistance in preparing aggregate statistics are in practice important use cases for some classification systems, neither is a necessity of classification or of ontology.
On the contrary: as is illustrated by our running example of a tag set for descriptions of characters classed by gender and age, a strictly hierarchical arrangement can easily hinder rather than aiding the analysis. We may, for example, choose to divide first by gender and then by age:
In this case, however, we will have no classes in the system in which we can find all babies, all children, all adolescents, or all adults. We could obtain such classes by reversing the order in which properties are used to subdivide the classes, but then we would have no class for all members of a given gender:
We will not belabor the point further. We believe that this simple example suffices to show that for practical use in some situations a hierarchical arrangement of classes will be more hindrance than help. We conclude that ontologies need not be trees, and that in some contexts they should not be trees.
Note also that annotation systems like CATMA allow the same passage to be annotated using more than one tag. It follows that the classification of text passages made explicit by a given collection of annotations cannot in any case be guaranteed to form a tree, because the same text passage may fall into multiple classes.
Are ontologies lattices?
If a hierarchy cannot be used to impose order on a tag set, what kind of organizing principle can be found to aid us in thinking about and navigating it? We believe a set of annotation classes can usefully be organized around the question “is the extension of tag A a subset of the extension of tag B?” or “is the intension of tag A a superset of the intension of tag B?” Such relations cannot always be organized into a hierarchy, but they can always be used as the organizing principle of a lattice.
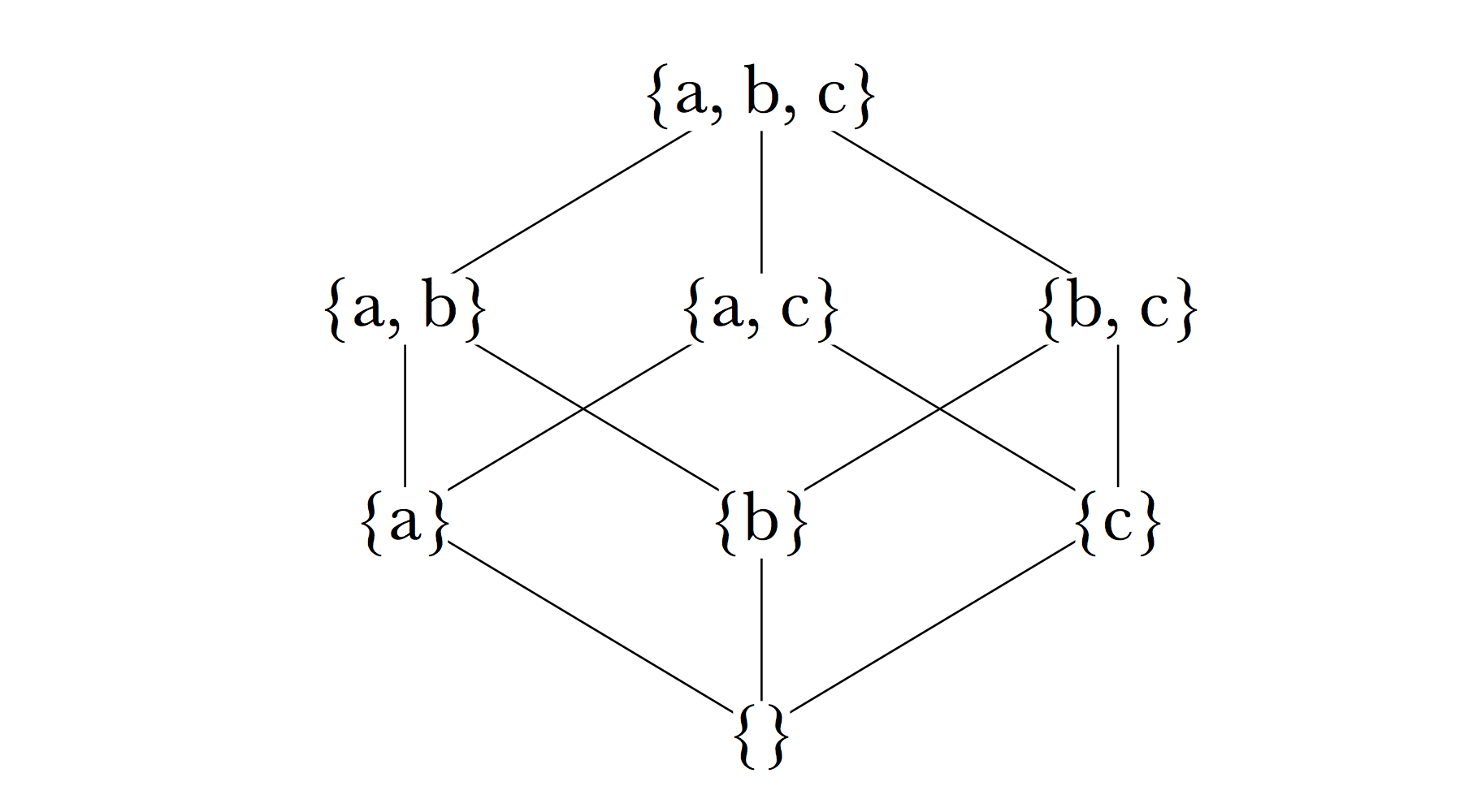
Mathematically, a lattice is described as an algebra satisfying certain constraints on two operators (or, equivalently, as any partially ordered set). The interested reader is directed to other sources for a full account; we content ourselves here with a few examples illustrating the salient features of lattices and showing how lattices can be formed from sets on the basis of the subset relation (which is, mathematically speaking, a partial ordering over the set of sets). If we consider the set {a, b, c} and all of its possible subsets, the resulting lattice can be drawn thus:[17]
As may be seen, each node in the lattice is a subset of those above it to which it is connected directly or indirectly by edges going upwards, and a superset of those to which it is connected by edges going downwards. The node at the top of the lattice, often written ⊤, is a superset of every node in the lattice and contains everything in the universe of discourse. The node at the bottom, often written ⊥, is the empty set (and thus guaranteed to be a subset of every node in the lattice). It may also be observed that a subset is directly connected to a superset by an edge only if there is no third set which is a superset of the first and subset of the second.
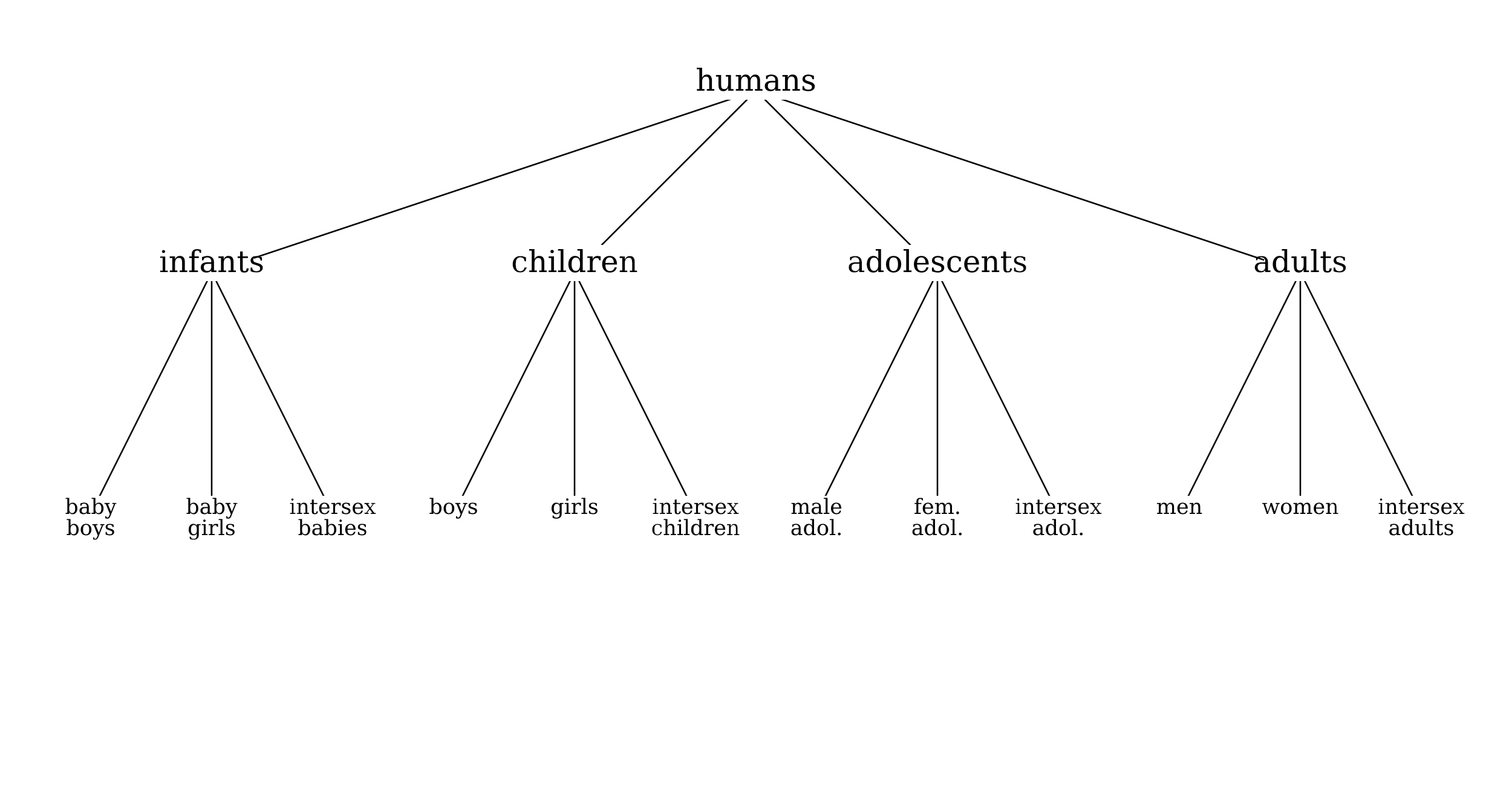
If we arrange sets of human characters (or, what comes out in this case to the same thing, sets of text passages referring to humans) into groups by age and gender stereotypes, distinguishing males, females, and intersex or third-sex individuals on the one hand and infants, children, adolescents, and adults on the other, then the sets can be visualized using the following demographic lattice. For simplicity, we assume that both gender and age are always either fully specified or not specified at all. It is possible to account for partially specified features in a lattice (a character who is not yet adolescent may be either an infant or a child), but doing so adds a lot of nodes to this lattice and does not much assist the reader.
It is not required that every combination of features be realized by a node in the lattice; if we defined tags only for all characters (all humans), female characters, children, third-sex characters, men, women, girls, and boys, the tags would form the following somewhat simpler lattice.
It is characteristic of all lattices that for any two nodes there is a unique nearest common ancestor, their meet, and a unique nearest common descendant, their join.[18] In the first lattice shown, the meet and join of any two sets are the union and intersection of the sets, respectively. In the two lattices showing demographic groupings of characters, the union and intersection of the sets represented by two nodes of the graph may or may not be present; the meet of men and children is the node humans, which is not the union of men and children but a superset of it. And in the second demographic lattice, the join of 3rd-sex and children is not their intersection but the empty set at the bottom of the lattice. It is guaranteed that in a lattice defined as these are by the subset relation, the meet of two nodes will be a superset of their union, and the join of two nodes will be a subset of their intersection.
Observe that just as menus and submenus can be structured hierarchically to match a hierarchical arrangement of annotation classes, so also the lattice diagram may be used to guide the creation of menus: each node n in the lattice will be represented by a menu choice, and each will have a submenu listing all the nodes below n and directly connected to n by an arc. The sole difference between the hierarchically arranged menus and those built from the lattice is that in the latter there may be more than one path from the top node of the lattice to a given tag. In the demographic lattices, the node for girls may be reached from the top node either by selecting first females and then girls, or by selecting first children and then girls.
In the tree-based system now used by CATMA, the supertags of any tag are always visible when their subtags are selected; in a lattice-based system, it might be convenient to provide a way to navigate from any tag to any of its supertags.
Observe also that inferences over annotation classes and text passages are supported by the lattice structure, in just the same way and for the same reasons as in a tree structure: the applicability of any subtag licenses an inference to the applicability of all of its supertags.
Defining annotation classes by operations on existing classes
CATMA allows the definition of a new tag (annotation class) either as a top-level tag in a tag set or as a subtag of an existing tag. This suffices for convenient definition of a hierarchy of classes, though additional facilities can be imagined.
To manage a tag set modeled as a lattice, interfaces like those now present in CATMA can be used, as well as the definition methods sketched in the section on the subtag/supertag relation for n-ary predicates above. As described there, for example, it would be convenient to be able to generate subtags for the possible values of the supertag's argument(s). From trope(x, y) with y ∈ {metaphor, metonymy, synecdoche, irony}, for example, it would be convenient to be able to generate four subtags metaphor(x), metonymy(x), synecdoche(x), and irony(x).[19] It would also be convenient if, in a related operation, existing instances of the supertag were retagged as instances of the new subtags, for the benefit of software unaware of the equivalence between the predicates trope(x, metaphor) and metaphor(x) and similar pairs.
Other methods of definition are also imaginable and may be desirable (assuming that the user interface can make the possibilities visible without confusing the user unaccustomed to looking at logical formulae).
- While retaining the subset/superset relation between the extension of the subtag and the extension of the supertag (and the inverse relation on their intensions), it would be convenient to be able to declare a new tag as a subtag of multiple supertags.One might, for example, define an annotation class for metaphors applied to female characters as a subtag both of female and of trope(x, metaphor).
- It would also be helpful to be able to add a new sub/super relation between existing tags.For example, if one has already defined annotation classes for metaphors and for metaphors-applied-to-women, and adds a new class for passages in which women are characterized, one might want to specify that the new class is a superclass of the existing class for metaphors-applied-to-women.(When this is done, the software would need to prune any existing arcs rendered redundant by the change. If the addition of a direct subtag/supertag link produces a situation in which tag A and B are both subtags of C, and A is also a subtag of B, then the direct subtag/supertag link between A and C should be removed. The software will also need to check for, and prevent, cycles in the subset/superset relation. It must not be the case that any class is directly or indirectly its own sub- or superclass.)
- It would be convenient to be able to define a new tag as the union or intersection of two or more existing tags (assuming that their union or intersection is not already present in the lattice). These operations make explicit the subset/superset relations holding among the supertags and the subtags (and by implication also the relations holding among the intensions of the classes).For example, in the smaller demographic lattice, a user might like to define a new tag males as the union of men and boys, or a new tag third-sex adults as the intersection of 3rd sex and adults.(In this case, too, the software will need to perform maintenance on the set of direct supertag/subtag links.)
Conclusion
We believe we have shown that in modelling ontologies for annotation systems like CATMA, lattices have advantages over trees. As other formalisms might of course also have been considered, our claim does not go beyond that.
Ontologies — both in general and in the context of textual annotation software — are not usefully defined as trees. They are more usefully defined as lattices.
Notes
[1] This paper began as a contribution to the 3d forTEXT workshop “Non-hierarchical concept ontologies and markup schemata”, held at the University of Hamburg on 24 and 25 January 2020. Our thanks go to Professor Jan Christoph Meister for the invitation, and to him as well as the other speakers at the workshop and the CATMA team for valuable comments and feedback.
[2] Some philosophers will object that ontology as pursued by Quine is not at all the same as the ontology pursued by earlier philosophers, i.e. a general theory about what kinds of things there are, but “a quite different set of preoccupations” [MacIntyre 1967].
[3] The philosopher Barry Smith suggests that “[m]ost prominent information-systems ontologists in recent years ... have come to hold that ontology deals not with reality itself but rather with ‘alternative possible worlds,’” [Smith 2003b, 160–161], and worries that “we must find ways to do justice to the fact that the different conceptualizations which serve as inputs to ontology are likely to be ... mutually inconsistent” [Smith 2003b, 162].
Quine's view was that ontology should be based on the theories and results of the natural sciences. Smith views some recent developments with concern: “... the running together of ontology and ontological commitments becomes strikingly less defensible when the ontological commitments of various specialist groups of nonscientists are allowed into the mix. How, ontologically, are we to treat the commitments of astrologists, or clairvoyants, or believers in leprechauns?” [Smith 2003b, 158].
Since annotation systems like CATMA do not seek to unify the disparate ontologies of different annotators, however, the problem of merging ontologies from different sources is not of immediate concern in the current context.
Quine's view was that ontology should be based on the theories and results of the natural sciences. Smith views some recent developments with concern: “... the running together of ontology and ontological commitments becomes strikingly less defensible when the ontological commitments of various specialist groups of nonscientists are allowed into the mix. How, ontologically, are we to treat the commitments of astrologists, or clairvoyants, or believers in leprechauns?” [Smith 2003b, 158].
Since annotation systems like CATMA do not seek to unify the disparate ontologies of different annotators, however, the problem of merging ontologies from different sources is not of immediate concern in the current context.
[4] A cautionary note is necessary at this point. If we allow classes or sets of things to be themselves objects of which we can predicate this or that property we may soon end up in situations known as Russell's Paradox. The set of all sets that are not members of themselves is both a member of itself and not a member of itself. Even predicates which do not hold of sets can be problematic if sets are involved in the definition, for example: the property “is a male barber who shaves all those males who do not shave themselves”
We will not elaborate on ways of avoiding this problem here; it suffices for our purpose to say that (we believe) Russell's Paradox will pose no danger for an annotation system in which annotations and the text passages to which they apply are disjoint sets. The addition of meta-annotations which apply to first-level annotations is also unproblematic, as long as meta-annotations cannot apply to meta-annotations, thus ensuring that the snake is kept from consuming its own tail.
We will not elaborate on ways of avoiding this problem here; it suffices for our purpose to say that (we believe) Russell's Paradox will pose no danger for an annotation system in which annotations and the text passages to which they apply are disjoint sets. The addition of meta-annotations which apply to first-level annotations is also unproblematic, as long as meta-annotations cannot apply to meta-annotations, thus ensuring that the snake is kept from consuming its own tail.
[5] As of December 2019, the number of estimated active users was more than 8,000 [Horstmann 2020, 160].
[6] In the following, we will refer to properties in CATMA as named properties, in order to distinguish properties as defined in CATMA from properties in general.
[7] Admittedly, CATMA does not enforce a single-rooted tree, but a single root can always be enforced on any CATMA tag set.
[8] The screenshots shown below come from the author's CATMA annotation of a snippet of [Spyri 1880] Heidi. The annotations have been made exclusively for illustrative purposes.
[9] If the search interface allows Boolean operations, as most serious search interfaces do, then both tag sets can express the same sets of searches, but not always with equal convenience. In this simple example, we believe a search for Male is more convenient than a search for Man OR Boy, and a search for Child more convenient than one for Girl or Boy. If the tag set has a finer granularity, the difference is more striking: using the lattice example given below, the choice is between allowing the query Male vs Baby_Boy OR Boy OR Male_Adolescent OR Man.
[10] A brief digression may be necessary here. In the usual case, the properties used to organize a classification scheme belong to the things being classified. In the case of annotations whose purpose is to ascribe some particular property to text passages, however, the relevant property is the one ascribed to the text passage — which may in turn reflect some property belonging to a character, object, or event mentioned or depicted in the text. In the novel Heidi, for example, the title character has the property (among others) of being a child; call that property Pc. Pc is a property belonging to human beings, whether real or imaginary, but not to text passages or annotations. A text passage mentioning Heidi, in turn, has the property (call it Pmc) of mentioning a child (that is, a character with property Pc). Property Pmc pertains to text passages, not to human beings or annotations. An annotation attributing property Pmc to a text passage has a property we might call Pamc: the property of attributing property Pmc to a text passage which mentions a character with property Pc. There are situations in which it is important to distinguish carefully among these three properties, but in practice there is seldom any confusion, precisely because they apply to very different classes of things.
Our usage is accordingly relaxed about the distinctions just made. When we describe the characteristic properties of annotation classes, it is normally simpler to focus on the properties being ascribed to the text passages annotated than to focus on the property pertaining to the annotation itself. Readers who prefer to avoid this metonymy may wish to mentally add the words “attributes to a text passage the property ...” at the beginning of a description.
Our usage is accordingly relaxed about the distinctions just made. When we describe the characteristic properties of annotation classes, it is normally simpler to focus on the properties being ascribed to the text passages annotated than to focus on the property pertaining to the annotation itself. Readers who prefer to avoid this metonymy may wish to mentally add the words “attributes to a text passage the property ...” at the beginning of a description.
[11] The nature of text passages and how they may most usefully be represented in electronic form are interesting and important questions but we will not attempt to address them here. CATMA provides an operational answer to these questions which is sufficiently functional to allow us to take “text passage” as a well defined concept for our discussion.
[12] It may seem like exaggeration to describe this class/subclass relation as a matter of logical inference, but we believe it is no exaggeration. It is a curious fact that most of the theorems proved by theorem-proving systems and logic programs have very little mathematical or philosophical interest, in part because from such a point of view they are seen as trivial. But the ability of logical inference to guide the operation of programs is nevertheless quite convenient for those who would like to have well behaved software with well defined operations.
[13] In practice CATMA represents a text passage not as an atomic value but as a structure with both an offset (starting point) and length. We elide the details, because for purposes of this discussion the internal structure of the representation of a text passage is immaterial.
[14] To avoid confusion, it should be observed that the imaginary tag sets we describe here and elsewhere are simplified examples; as any attempt to apply them in practice will show, a tag set intended for practical use will want tags or property values to handle cases where the text describes a group of people of mixed ages or genders, cases where the gender or age of the person(s) described is indeterminate, and so on.
[15] In the current version of CATMA (as far as we know), named properties are not inherited by subtags, there is no option to restrict the set of possible values to the values listed, and there is no facility for supplying values automatically, as is suggested here.
[16] The paper, which recommends that ontologies should be organized as networks consisting of top-, mid-, and lower-level ontologies, says specifically about mid-level ontologies that they should “consist of terms which are organized in strict subclass hierarchies starting from more and proceeding to less general; either in one such hierarchy, or in multiple separate hierarchies representing multiple axes of classification ...” [Rudnicki et al. 2016].
With the phrase “or in multiple separate hierarchies”, Rudnicki et al. appear to be suggesting that in practice multiple ontologies will need to be deployed. We don't think this is a very helpful idea in the context of CATMA or similar systems: if the tags Girl and Boy are placed both in a gender-age hierarchy and in an age-gender hierarchy, then every operation on the tag set that could be guided by the structure of the ontology (on which see further below) must become more complicated, either by asking the user which ontology to use, or by requiring the operation to take multiple ontologies into account.
Barry Smith (whom we quoted earlier) is one of the coauthors of this white paper; he is more explicit about the importance of trees in what appears to be a longer draft for [Smith 2003b]. Here, he is quite insistent that “A taxonomy should take the form of a tree in the mathematical sense.” His strongest reason for this insistence seems to be that “... a classification should involve no double-counting” [Smith 2003a, 11, 12].
With the phrase “or in multiple separate hierarchies”, Rudnicki et al. appear to be suggesting that in practice multiple ontologies will need to be deployed. We don't think this is a very helpful idea in the context of CATMA or similar systems: if the tags Girl and Boy are placed both in a gender-age hierarchy and in an age-gender hierarchy, then every operation on the tag set that could be guided by the structure of the ontology (on which see further below) must become more complicated, either by asking the user which ontology to use, or by requiring the operation to take multiple ontologies into account.
Barry Smith (whom we quoted earlier) is one of the coauthors of this white paper; he is more explicit about the importance of trees in what appears to be a longer draft for [Smith 2003b]. Here, he is quite insistent that “A taxonomy should take the form of a tree in the mathematical sense.” His strongest reason for this insistence seems to be that “... a classification should involve no double-counting” [Smith 2003a, 11, 12].
[17] This method of visualizing a lattice is a Hasse diagram, named after the mathematician Helmut Hasse (1898-1979). For any pair of nodes n1 and n2, if n1 ≤ n2, then n2 is drawn higher in the diagram than n1, and an arc connects them (necessarily running upward) just in case there is no third node n3 in the lattice such that n1 ≤ n3 ≤ n2. (In all the lattices we discuss, the partial ordering is given by the subset relation, so the rule just stated could be restated in terms of n1 ⊆ n2, etc.)
The arcs in a Hasse diagram show the transitive reduction of the partial ordering on the set, and that any directed acyclic graph has a unique transitive reduction. If we think of the arcs in a graph as providing pathways to allow travel from one node to another, the transitive reduction is calculated by pruning away every direct connection that connects two nodes already connected by other means, to reduce the number of arcs to the minimum that preserves all the travel possibilities of the original graph.
The arcs in a Hasse diagram show the transitive reduction of the partial ordering on the set, and that any directed acyclic graph has a unique transitive reduction. If we think of the arcs in a graph as providing pathways to allow travel from one node to another, the transitive reduction is calculated by pruning away every direct connection that connects two nodes already connected by other means, to reduce the number of arcs to the minimum that preserves all the travel possibilities of the original graph.
[18] We use the term ancestor informally to denote a node reachable from another node by following one or more edges in an uphill direction, and descendant to mean the converse, a node reachable by going downhill.
[19] Their characteristic predicates would then be trope(x, metaphor), trope(x, metonymy), trope(x, synecdoche), and trope(x, irony). (This only makes sense, of course, if the user has enumerated a set of possible values for the named property, rather than merely enumerating sample values. In the current version of CATMA, we do not believe the user can make this distinction reliably.)
Works Cited
Gius et al. 2022 Gius, E., Meister, J.C., Meister, M.,
Petris, M., Bruck, C., Jacke, J., Schumacher, M., Gerstorfer, D., Flüh, M., Horstmann,
J. (2022): CATMA 6 (Version 6.5). Zenodo. DOI:
10.5281/zenodo.1470118. Available at https://catma.de/
Horstmann 2020 Horstmann, J.,
“Undogmatic Literary Annotation with CATMA”. In: Julia Nantke and
Frederik Schlupkothen (eds.), Annotations in Scholarly Editions
and Research, De Gruyter 2020. Available at
https://doi.org/10.1515/9783110689112-008
MacIntyre 1967 MacIntyre, A.,
“Ontology,” in The encyclopedia of
philosophy. New York: Macmillan, 1967, vol. 5. Available at
“Ontology, history of” at
https://www.encyclopedia.com/humanities/encyclopedias-almanacs-transcripts-and-maps/ontology-history.
Quine 1948 Quine, W.v.O., “On
what there is”. Review of Metaphysics 1948. Reprinted in
From a logical point of view., pp 1-19. Cambridge: Harvard
University Press, 1953.
Rudnicki et al. 2016 Rudnicki, R. Smith, B., Malyuta,
T., and Mandrick, W., “Best Practices of Ontology
Development” White Paper, CUBRC Advantage Through Technology, 2016.
Available at https://www.nist.gov/system/files/documents/2019/05/30/nist-ai-rfi-cubrc_inc_002.pdf.
Smith 2003a Smith, B.,
“Ontology and information systems,”.
Available at http://ontology.buffalo.edu/ontology_long.pdf.
Smith 2003b Smith, b.
“Ontology,” in Blackwell guide to the
philosophy of computing and information, ed. Luciano Floridi. Oxford: Blackwell, 2003.
Available at https://philpapers.org/archive/SMIO-11.pdf.
Spyri 1880 Spyri, J.,
Heidis Lehr- und Wanderjahre, 1880. Available at
https://www.gutenberg.org/ebooks/7511
Webster's 1923
Webster's new international dictionary of the English language,
ed. W. T. Harris and F. Sturgis Allen. Springfield, Mass.: G. & C. Merriam Co, 1923.